-
CHƯƠNG 1. SỐ HỮU TỈ - SỐ THỰC
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC – ĐƯỜNG THẲNG SONG SONG
-
CHƯƠNG 2. TAM GIÁC
-
Chủ đề 3: Tam giác - Tam giác bằng nhau
- 1. Tổng ba góc trong một tam giác
- 2. Hai tam giác bằng nhau
- 3. Trường hợp bằng nhau thứ nhất của tam giác: Cạnh - cạnh - cạnh (c.c.c)
- 4. Trường hợp bằng nhau thứ hai của tam giác: Cạnh - góc - cạnh (c.g.c)
- 5. Trường hợp bằng nhau thứ ba của tam giác: Góc - góc - góc (g.g.g)
- Bài tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
- Luyện tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
-
Chủ đề 4. Tam giác cân - Định lý Pythagore
-
Ôn tập chương 2 - Hình học 7
-
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4. BIỂU THỨC ĐẠI SỐ
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC – CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
-
Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
- 1. Quan hệ giữa góc và cạnh trong một tam giác
- 2. Quan hệ giữa đường vuông góc và đường xiên – Giữa đường xiên và hình chiếu
- 3. Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- Bài tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
- Luyện tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
-
Chủ đề 6 : Các đường đồng quy của tam giác
- 1. Tính chất ba đường trung tuyến của tam giác
- 2. Tính chất tia phân giác của một góc
- 3. Tính chất ba đường phân giác của tam giác
- 4. Tính chất đường trung trực của một đoạn thẳng
- 5. Tính chất ba đường trung trực của tam giác
- 6. Tính chất ba đường cao trong tam giác
- Bài tập - Chủ đề 6 : Các đường đồng quy của tam giác
- Luyện tập - Chủ đề 6 : Các đường đồng quy của tam giác
-
Ôn tập chương 3 – Hình học
-
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 7
Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
Bài tập - Chủ đề 6 : Các đường đồng quy của tam giác
Bài tập 7 trang 120 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Chứng minh rằng : Trong một tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.
Đề bài
Chứng minh rằng : Trong một tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.
Lời giải chi tiết
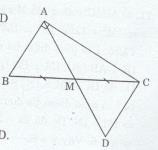
Trên tia đối của tia MA lấy điểm D sao cho MA = MD
Xét ∆ABM và ∆MCD ta có:
BM = MC (M là trung điểm của BC)
AM = MD (cách vẽ)
Và \(\widehat {AMB} = \widehat {CMD}\) (hai góc đối đỉnh)
Do đó: ∆ABM = ∆DCM (c.g.c) \( \Rightarrow \widehat {BAM} = \widehat {MDC}\)
Mà \(\widehat {BAM}\) và\(\widehat {MDC}\) ở vị trí so le trong. Do đó AB // CD.
Ta có AB // CD, \(AB \bot AC\) (∆ABC vuông tại A) \( \Rightarrow CD \bot AC \Rightarrow \widehat {ACD} = 90^\circ\)
Xét ∆ACD và ∆ABC ta có: CD = AB (vì ∆DCM = ABM)
\(\widehat {ACD} = \widehat {BAC}( = 90^\circ )\)
AC là cạnh chung
Do đó: ∆ACD = ∆CAB (c.g.c) => AD = BC
Mà \(AM = {1 \over 2}AD(MA = MD)\). Do đó \(AM = {1 \over 2}BC.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài tập 8 trang 120 Tài liệu dạy – học Toán 7 tập 2
- Bài tập 9 trang 121 Tài liệu dạy – học Toán 7 tập 2
- Bài tập 10 trang 121 Tài liệu dạy – học Toán 7 tập 2
- Bài tập 11 trang 121 Tài liệu dạy – học Toán 7 tập 2
- Bài tập 12 trang 121 Tài liệu dạy – học Toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
