-
CHƯƠNG 1. SỐ HỮU TỈ - SỐ THỰC
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC – ĐƯỜNG THẲNG SONG SONG
-
CHƯƠNG 2. TAM GIÁC
-
Chủ đề 3: Tam giác - Tam giác bằng nhau
- 1. Tổng ba góc trong một tam giác
- 2. Hai tam giác bằng nhau
- 3. Trường hợp bằng nhau thứ nhất của tam giác: Cạnh - cạnh - cạnh (c.c.c)
- 4. Trường hợp bằng nhau thứ hai của tam giác: Cạnh - góc - cạnh (c.g.c)
- 5. Trường hợp bằng nhau thứ ba của tam giác: Góc - góc - góc (g.g.g)
- Bài tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
- Luyện tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
-
Chủ đề 4. Tam giác cân - Định lý Pythagore
-
Ôn tập chương 2 - Hình học 7
-
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4. BIỂU THỨC ĐẠI SỐ
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC – CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
-
Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
- 1. Quan hệ giữa góc và cạnh trong một tam giác
- 2. Quan hệ giữa đường vuông góc và đường xiên – Giữa đường xiên và hình chiếu
- 3. Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- Bài tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
- Luyện tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
-
Chủ đề 6 : Các đường đồng quy của tam giác
- 1. Tính chất ba đường trung tuyến của tam giác
- 2. Tính chất tia phân giác của một góc
- 3. Tính chất ba đường phân giác của tam giác
- 4. Tính chất đường trung trực của một đoạn thẳng
- 5. Tính chất ba đường trung trực của tam giác
- 6. Tính chất ba đường cao trong tam giác
- Bài tập - Chủ đề 6 : Các đường đồng quy của tam giác
- Luyện tập - Chủ đề 6 : Các đường đồng quy của tam giác
-
Ôn tập chương 3 – Hình học
-
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 7
Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
B. Phần hình học
Bài tập 1 trang 130 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC cân tại A có AM là trung tuyến. Đường cao BE cắt AM tại H. Chứng minh CH vuông góc với AB.
Đề bài
Cho tam giác ABC cân tại A có AM là trung tuyến. Đường cao BE cắt AM tại H. Chứng minh CH vuông góc với AB.
Phương pháp giải - Xem chi tiết
3 đường cao trong 1 tam giác đồng quy.
Lời giải chi tiết
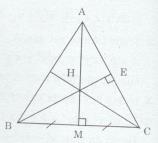
∆ABC cân tại A có AM là đường trung tuyến (gt)
=> AM cũng là đường cao của ∆ABC
Mà BE là đường cao của ∆ABC (gt)
Và BE cắt AM tại H (gt)
Nên H là trực tâm của ∆ABC
=> CH là đường cao của ∆ABC
\( \Rightarrow CH \bot AB.\)
Bình luận
Chia sẻ
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
