 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 1. Nhắc lại và bổ sung các khái niệm về hàm số
Bài 1. Nhắc lại và bổ sung các khái niệm về hàm số
Bài 5 trang 45 SGK Toán 9 tập 1
Vẽ đồ thị hàm số y = x
Đề bài
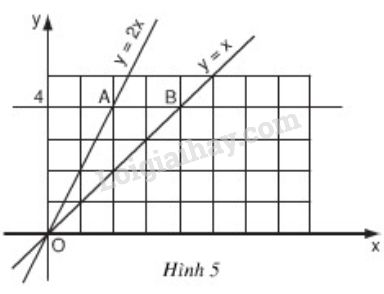
a) Vẽ đồ thị hàm số \(y = x\) và \(y =2x\) trên cùng một mặt phẳng tọa độ \(Oxy\) \((h.5)\).
b) Đường thẳng song song với trục \(Ox\) và cắt trục \(Oy\) tại điểm có tung độ \(y = 4\) lần lượt cắt các đường thẳng \(y = 2x,\ y = x\) tại hai điểm \(A\) và \(B\).
Tìm tọa độ của các điểm \(A,\ B\) và tính chu vi, diện tích của tam giác \(OAB\) theo đơn vị đo trên các trục tọa độ là xentimét.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Cách vẽ đồ thị hàm số \(y=ax,\ (a \ne 0)\): Cho \(x=x_0 \Rightarrow y_0=ax_0\)
Đồ thị hàm số \(y=ax\, \, (a\neq 0)\) là đường thẳng đi qua gốc tọa độ và điểm \(A(x_0;y_0)\)
b) +) Đường thẳng song song với trục \(Ox\) cắt trục \(Oy\) tại điểm có tung độ \(y=b\) có phương trình đường thẳng là \(y=b.\)
+) Muốn tìm tọa độ giao điểm của hai đường thẳng \(y=ax\) và \(y=a'x\) ta giải phương trình \(ax=a'x\) tìm được hoành độ. Thay hoành độ vào một trong hai đường thẳng trên tìm được tung độ.
+) Sử dụng đinh lí Py - ta - go trong tam giác vuông: \(\Delta ABC\) vuông tại \(A\) thì \(AB^2+ AC^2 =BC^2\).
+) Chu vi tam giác: \(C_{∆OAB}= AB+BO+AO.\)
+) Diện tích \(\Delta ABC\) có đường cao \(h\) và \(a\) là độ dài cạnh ứng với đường cao: \(S_{∆OAB}=\dfrac{1}{2}.h.a\)
Lời giải chi tiết
a) Xem hình trên và vẽ lại
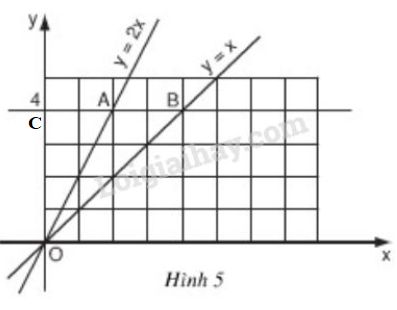
b)
+) Ta coi mỗi ô vuông trên hình \(5\) là một hình vuông có cạnh là \(1cm\).
Từ hình vẽ ta xác định được: \(A(2; 4),\ B(4; 4)\).
+) Tính độ dài các cạnh của \(∆OAB\):
Dễ thấy \(AB = 4 - 2 = 2\) \((cm)\).
Gọi \(C\) là điểm nằm trên trục tung, có tung độ là \(4\), ta có \(OC=4cm,AC=2cm;BC=4cm\)
Áp dụng định lý Py-ta-go cho các tam giác vuông \(OAC\) và \(OBC\), ta có:
\(\eqalign{
& OA = \sqrt {{AC^2} + {OC^2}} = \sqrt {{2^2} + {4^2}} = 2\sqrt 5 \left( {cm} \right) \cr
& OB = \sqrt {{BC^2} + {OC^2}}= \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \left( {cm} \right) \cr} \)
\(\Rightarrow\) Chu vi \(\Delta OAB\) là:
\(C_{\Delta OAB}=OA + OB + AB \)
\(=2+ 2\sqrt 5 + 4\sqrt 2 \approx 12,13(cm)\)
+) Tính diện tích \(∆OAB\):
Cách 1:
\(\eqalign{
& {S_{\Delta OAB}} = {S_{\Delta OBC}} - {S_{\Delta OAC}} \cr
& = {1 \over 2}OC.BC - {1 \over 2}OC.AC \cr
& = {1 \over 2}{.4^2} - {1 \over 2}.4.2 = 8 - 4 = 4\left( {c{m^2}} \right) \cr} \)
Cách 2:
\(∆OAB\) có đường cao ứng với cạnh \(AB\) là \(OC\).
\( \Rightarrow S_{∆OAB}=\dfrac{1}{2}.OC.AB=\dfrac{1}{2}.4.2=4\) \((cm^2)\)
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận