 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh v..
Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh v..
Bài 26 trang 119 SGK Toán 9 tập 2
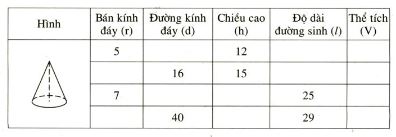
Hãy điền đầy đủ vào các ô trống cho ở bảng sau (đơn vị độ dài: cm)
Đề bài
Hãy điền đầy đủ vào các ô trống cho ở bảng sau (đơn vị độ dài: cm):
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Cho hình nón có chiều cao \(h,\) bán kính đáy \(r\) và đường sinh \(l.\) Khi đó:
+) Đường kính đáy: \(d=2r.\)
+) Thể tích hình nón: \(V=\dfrac{1}{3} \pi r^2h.\)
+) Mối quan hệ \(l^2=h^2+r^2.\)
Lời giải chi tiết
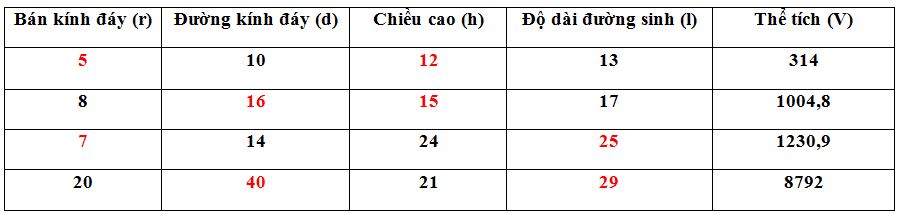
Cách tính:
Lấy \(\pi=3,14\)
+ Dòng thứ nhất: Khi \(r = 5cm;h = 12cm\) ta có
- Đường kính \(d = 2r = 2.5 = 10cm\)
- Đường sinh \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{5^2} + {{12}^2}} = 13\,cm\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.5^2}.12 = 100\pi=314 \left( {c{m^3}} \right)\)
+ Dòng thứ hai: Khi \(d = 16cm;h = 15cm\) ta có
- Bán kính \(r = \dfrac{d}{2} = \dfrac{{16}}{2} = 8cm\)
- Đường sinh \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{8^2} + {{15}^2}} = 17\,cm\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.8^2}.15 = 320\pi =1004,8\left( {c{m^3}} \right)\)
+ Dòng thứ ba: Khi \(r = 7cm;l = 25cm\) ta có
- Đường kính \(d = 2r = 2.7 = 14cm\)
- Vì \({l^2} = {h^2} + {r^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} = \sqrt {{{25}^2} - {7^2}} = 24cm\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.7^2}.24 = 392\pi \approx 1230,9\left( {c{m^3}} \right)\)
+ Dòng thứ tư: Khi \(d = 40cm;l = 29cm\) ta có
- Đường kính \(r = \dfrac{d}{2} = \dfrac{{40}}{2} = 20cm\)
- Vì \({l^2} = {h^2} + {r^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} = \sqrt {{{29}^2} - {{20}^2}} = 21cm\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.20^2}.21 = 2800\pi =8792 \left( {c{m^3}} \right)\)
Các bài khác cùng chuyên mục












Danh sách bình luận