Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7 Bài tập - Chủ đề 4: Tam giác cân. Định lý Pythagore

Bài 20 trang 170 Tài liệu dạy – học Toán 7 tập 1


Giải bài tập Cho tam giác MNP vuông tại M. Tia phân giác của góc N cắt MP tại E.

Đề bài

Cho tam giác MNP vuông tại M. Tia phân giác của góc N cắt MP tại E. Kẻ \(EF \bot NP(F \in NP).\)

a) Chứng minh rằng tam giác MNF cân.

b) Kẻ \(MH \bot NP.\)  Chứng minh rằng MF là phân giác của góc HME.

Lời giải chi tiết

 

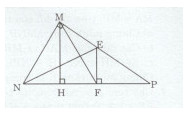
a)Xét tam giác MNE vuông tại M và tam giác NEF vuông tại F ta có:

\(\widehat {MNE} = \widehat {FNE}\)   (NE là tia phân giác của góc MNF)

NE là cạnh chung.

Do đó: \(\Delta MNE = \Delta FNE\)  (cạnh huyền - góc nhọn)

=>MN = NF => tam giác MNF cân tại N.

b) Ta có: \(ME = EF(\Delta MNE = \Delta FNE)\)

=>Tam giác MEF cân tại E \(\Rightarrow \widehat {EMF} = \widehat {EFM}\)

Mặt khác \(MH \bot NP(gt);EF \bot NP(gt)\)

\(\Rightarrow MH//EF \Rightarrow \widehat {HMF} = \widehat {EFM}\)   (hai góc so le trong).

Mà \(\widehat {EMF} = \widehat {EFM}(cmt) \Rightarrow \widehat {HMF} = \widehat {EMF}\)

Vậy MF là tia phân giác của góc HME.

Loigiaihay.com


Bình chọn:
3.4 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store