Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7 Bài tập - Chủ đề 4: Tam giác cân. Định lý Pythagore

Bài 1 trang 168 Tài liệu dạy – học Toán 7 tập 1


Giải bài tập Trong các tam giác ở các hình 15a, b, c, d, tam giác nào là tam giác cân, tam giác nào là tam giác đều ? Vì sao ?

Đề bài

Trong các tam giác ở các hình 15a, b, c, d, tam giác nào là tam giác cân, tam giác nào là tam giác đều ? Vì sao ?

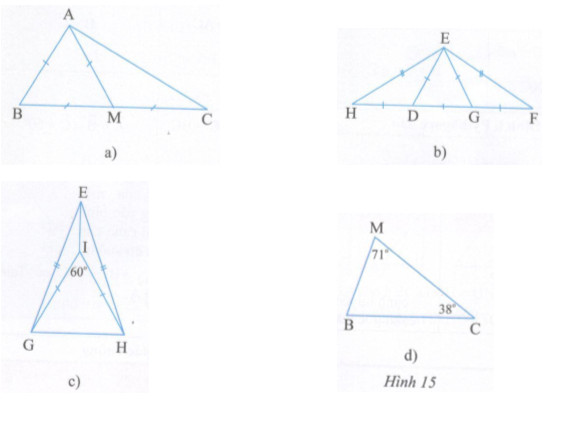
Lời giải chi tiết

a)Ta có: AB = BM = AM (gt) => tam giác ABM đều.

AM = CM (gt) => tam giác MAC cân tại M.

b) Ta có: ED = DG = EG (gt) => tam giác EDG đều.

DH = DE => tam giác DEH cân tại D.

Ta có: EG = GF => tam giác GEF cân tại G.

Ta có: EH = EF => tam giác EHF cân tại E.

c) Ta có: IG = IH (gt) => tam giác IGH cân tại I. Mà \(\widehat {GIH} = {60^0}(gt).\)   Do đó tam giác IGH đều.

Ta có: EG = EH (gt) => tam giác EGH cân tại E.

d) Tam giác MBC có: \(\widehat M + \widehat B + \widehat C = {180^0}\)

Do đó: \({71^0} + \widehat B + {38^0} = {180^0} \Rightarrow \widehat B = {180^0} - {71^0} - {38^0} = {71^0}.\)

Ta có: \(\widehat B = \widehat M( = {71^0}) \Rightarrow \Delta CBM\)  cân tại C.

Loigiaihay.com


Bình chọn:
4.2 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store