Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7 Bài tập - Chủ đề 4: Tam giác cân. Định lý Pythagore

Bài 12 trang 169 Tài liệu dạy – học Toán 7 tập 1


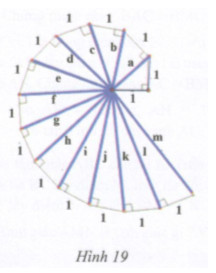
Giải bài tập Lần lượt tính độ dài các cạnh huyền a, b, c, d của các tam giác vuông theo hình 19. Hãy dự đoán kết quả của các cạnh huyền còn lại.

Đề bài

Lần lượt tính độ dài các cạnh huyền a, b, c, d của các tam giác vuông theo hình 19. Hãy dự đoán kết quả của các cạnh huyền còn lại.

Lời giải chi tiết

Áp dụng định lý Pythagore cho tam giác vuông, ta có:

\({a^2} = {1^2} + {1^2} = 2.\)   Mà a > 0 do đó: \(b = \sqrt 2 .\)

\({b^2} = {1^2} + {a^2} = 1 + 2 = 3.\)  . Mà b > 0 do đó \(b = \sqrt 3 .\)

\({c^2} = {b^2} + 1 = 3 + 1 = 4.\)   Mà c > 0 do đó: \(c = \sqrt 4  = 2.\)

\({d^2} = {c^2} + {1^2} = 4 + 1 = 5.\)   Mà d > 0 do đó: \(d = \sqrt 5 .\)

Dự đoán độ dài các cạnh huyền còn lại lần lượt là:

\(\eqalign{  & e = \sqrt 6 ,f = \sqrt 7 ,g = \sqrt 8 ,h = \sqrt 9  = 3  \cr  & i = \sqrt {10} ,j = \sqrt {11} ,k = \sqrt {12}   \cr  & l = \sqrt {13} ,m = \sqrt {14}  \cr} \)

Loigiaihay.com


Bình chọn:
4.2 trên 5 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store