Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7 Bài tập - Chủ đề 4: Tam giác cân. Định lý Pythagore

Bài 11 trang 169 Tài liệu dạy – học Toán 7 tập 1


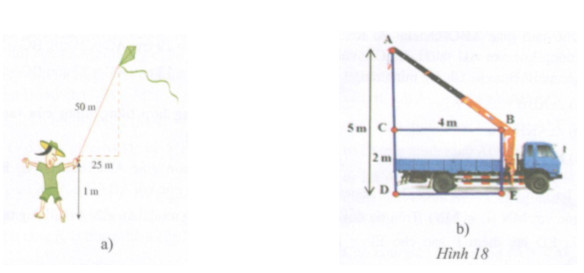
Giải bài tập a) Tính độ cao của con diều so với mặt đất (h.18a).

Đề bài

a) Tính độ cao của con diều so với mặt đất (h.18a).

b) Tính chiều dài cần cẩu AB (h.18b).

                                     

Lời giải chi tiết

a)Gọi độ cao của con diều so với tay người thả là h (m).

Áp dụng định lý Pythagore trong tam giác vuông ta có: \({h^2} + {25^2} = {50^2}.\)

\(\Rightarrow {h^2} = {50^2} - {25^2} = 2500 - 625 = 1875\)

Mà h > 0 do đó \(h = \sqrt {1875} \approx 43,3 (m)\)

Độ cao của con diều so với mặt đất là: \(43,3  + 1 = 44,3 (m).\)

b) \(AC = AD - CD = 5 - 2 = 3(m)\)

Áp dụng định lý Pythagore cho tam giác ABC vuông tại C ta có: \(A{B^2} = A{C^2} + B{C^2}\)

Do đó: \(A{B^2} = {3^2} + {4^2} = 9 + 16 = 25\)

Mà AB > 0 nên \(AB = \sqrt {25}  = 5(m).\)   Vậy chiều dài của cần cẩu là 5m.


Bình chọn:
4.2 trên 9 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store