Lý thuyết về tỷ số lượng giác của góc nhọn

Tổng hợp Đề thi vào 10 có đáp án và lời giải

Toán - Văn - Anh

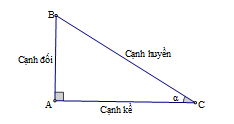
1. Kiến thức cần nhớ

$\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};$

$\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}$.

Tính chất 1:

+ Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Tức là: Cho hai góc $\alpha ,\beta $ có $\alpha + \beta = {90^0}$

Khi đó:

$\sin \alpha = \cos \beta ;\cos \alpha = \sin \beta ;$ $\tan \alpha = \cot \beta ;\cot \alpha = \tan \beta $.

Tính chất 2:

+ Nếu hai góc nhọn $\alpha $ và $\beta $ có $\sin \alpha = \sin \beta $ hoặc $\cos \alpha = \cos \beta $ thì $\alpha = \beta $

Tính chất 3:

+ Nếu $\alpha $ là một góc nhọn bất kỳ thì

$0 < \sin \alpha < 1;0 < \cos \alpha < 1,$ $\tan \alpha > 0;\cot \alpha > 0$

${\sin ^2}\alpha + {\cos ^2}\alpha = 1;$ $\tan \alpha .\cot \alpha = 1$

$\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }};$

$1 + {\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }};1 + {\cot ^2}\alpha = \dfrac{1}{{{{\sin }^2}\alpha }}$

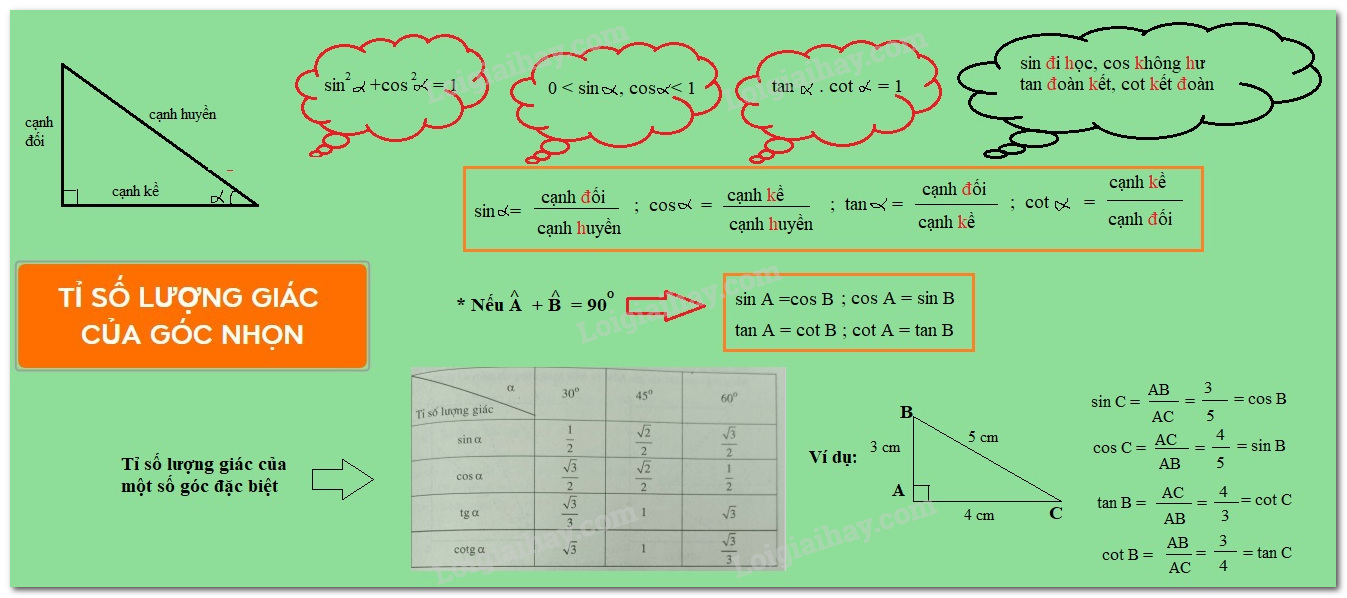
Bảng tỉ số lượng giác các góc đặc biệt

2. Các dạng toán thường gặp

Dạng 1: Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc

Phương pháp:

Sử dụng các tỉ số lượng giác của góc nhọn, định lý Py-ta-go, hệ thức lượng trong tam giác vuông để tính toán các yếu tố cần thiết.

Dạng 2: So sánh các tỉ số lượng giác giữa các góc

Phương pháp:

Bước 1 : Đưa các tỉ số lượng giác về cùng loại (sử dụng tính chất "Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia")

Bước 2: Với góc nhọn $\alpha ,\,\beta $ ta có: $\sin \alpha < \sin \beta \Leftrightarrow \alpha < \beta ;$$\cos \alpha < \cos \beta \Leftrightarrow \alpha > \beta ;$

$\tan \alpha < \tan \beta \Leftrightarrow \alpha < \beta ;$$\cot \alpha < \cot \beta \Leftrightarrow \alpha > \beta $.

Dạng 3: Rút gọn, tính giá trị biểu thức lượng giác

Phương pháp:

Ta thường sử dụng các kiến thức

+ Nếu $\alpha $ là một góc nhọn bất kỳ thì

$0 < \sin \alpha < 1;0 < \cos \alpha < 1$, $\tan \alpha > 0;\cot \alpha > 0$ , ${\sin ^2}\alpha + {\cos ^2}\alpha = 1;\tan \alpha .\cot \alpha = 1$

$\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }};$

$1 + {\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }};1 + {\cot ^2}\alpha = \dfrac{1}{{{{\sin }^2}\alpha }}$

+ Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.