-
PHẦN ĐẠI SỐ - TOÁN 9 TẬP 1
-
CHƯƠNG I. CĂN BẬC HAI. CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng Căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo)
- Bài 8. Rút gọn biểu thức chứa căn bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương I – Căn bậc hai. Căn bậc ba
- Đề kiểm tra 15 phút - Chương I - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương I - Đại số 9
-
CHƯƠNG II. HÀM SỐ BẬC NHẤT
- Bài 1. Nhắc lại và bổ sung các khái niệm về hàm số
- Bài 2. Hàm số bậc nhất
- Bài 3. Đồ thị của hàm số y = ax + b (a ≠ 0)
- Bài 4. Đường thẳng song song và đường thẳng cắt nhau
- Bài 5. Hệ số góc của đường thẳng y = ax + b (a ≠ 0).
- Ôn tập chương II – Hàm số bậc nhất
- Đề kiểm tra 15 phút - Chương 2 - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Đại số 9
-
-
PHẦN HÌNH HỌC - TOÁN 9 TẬP 1
-
CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
- Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Bài 2. Tỉ số lượng giác của góc nhọn
- Bài 3. Bảng lượng giác
- Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
- Bài 5. Ứng dụng thực tế các tỉ số lượng giác của góc nhọn. Thực hành ngoài trời
- Ôn tập chương I – Hệ thức lượng giác trong tam giác vuông
- Đề kiểm tra 15 phút - Chương 1 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Hình học 9
-
CHƯƠNG II. ĐƯỜNG TRÒN
- Bài 1. Sự xác định của đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
- Ôn tập chương II – Đường tròn
- Đề kiểm tra 15 phút - Chương 2 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Hình học 9
-
-
Đề cương ôn tập học kì 1
-
Đề thi học kì 1 mới nhất có lời giải
-
PHẦN ĐẠI SỐ - TOÁN 9 TẬP 2
-
CHƯƠNG III. HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
- Bài 1. Phương trình bậc nhất hai ẩn
- Bài 2. Hệ hai phương trình bậc nhất hai ẩn
- Bài 3. Giải hệ phương trình bằng phương pháp thế
- Bài 4. Giải hệ phương trình bằng phương pháp cộng đại số.
- Bài 5. Giải bài toán bằng cách lập hệ phương trình
- Bài 6. Giải bài toán bằng cách lập hệ phương trình (Tiếp theo)
- Ôn tập Chương III Hệ hai phương trình bậc nhất hai ẩn
- Đề kiểm 15 phút - Chương 3 - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Đại số 9
-
CHƯƠNG IV. HÀM SỐ y = ax^2 (a ≠ 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số y = ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số y = ax^2 (a ≠ 0).
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Ôn tập chương IV - Hàm số y = ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
- Đề kiểm tra 15 phút - Chương 4 - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 4 - Đại số 9
-
-
PHẦN HÌNH HỌC - TOÁN 9 TẬP 2
-
CHƯƠNG III. GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Ôn tập chương III – Góc với đường tròn
- Đề kiểm tra 15 phút - Chương 3 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Hình học 9
-
CHƯƠNG IV. HÌNH TRỤ - HÌNH NÓN - HÌNH CẦU
- Bài 1. Hình trụ - Diện tích xung quanh và thể tích hình trụ
- Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Bài 3. Hình cầu. Diện tích hình cầu và thể tích hình cầu
- Ôn tập chương IV – Hình trụ - Hình nón – Hình cầu
- Đề kiểm tra 45 phút (1 tiết) - Chương 4 - Hình học 9
-
BÀI TẬP ÔN CUỐI NĂM - TOÁN 9
-
-
Đề thi học kì 2 mới nhất có lời giải
-
Đề cương ôn tập học kì 2
-
Câu hỏi tự luyện Toán 9
-
Tải 30 đề kiểm tra giữa kì 1 Toán 9
-
Tải 30 đề ôn tập học kì 1 Toán 9
-
Tải 30 đề thi học kì 1 của các trường Toán 9
-
Tải 30 đề kiểm tra giữa kì 2 Toán 9
-
Tải 30 đề ôn tập học kì 2 Toán 9
-
Tải 30 đề thi học kì 2 của các trường Toán 9
Bài 11 trang 76 SGK Toán 9 tập 1
Tính các tỷ số lượng giác của góc B, từ đó suy ra các tỷ số lượng giác của góc A.
Đề bài
Cho tam giác \(ABC\) vuông tại \(C\), trong đó \(AC=0,9m\), \(BC=1,2m\). Tính các tỷ số lượng giác của góc \(B\), từ đó suy ra các tỷ số lượng giác của góc \(A\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Dùng định lí Pytago để tính độ dài cạnh huyền.
+) Dựa vào định nghĩa tỉ số lượng giác để tính các tỉ số lượng giác của góc \(B\).
\(\sin \alpha =\dfrac{cạnh\ đối}{cạnh\ huyền};\) \(\cos \alpha = \dfrac{cạnh\ kề}{cạnh\ huyền}\);
\(\tan \alpha = \dfrac{cạnh\ đối}{cạnh\ kề};\) \(\cot \alpha =\dfrac{cạnh\ kề}{cạnh\ đối}.\)
+) Dựa vào định lí về tỉ số lượng giác của hai góc phụ nhau: " Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tan góc này bằng cotang góc kia" để từ các tỉ số lượng giác của góc \(B\) tính tỉ số lượng giác của góc \(A\).
Lời giải chi tiết
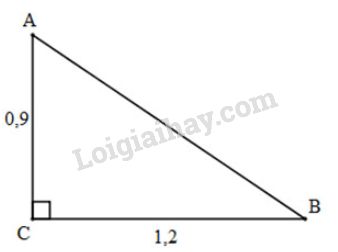
Xét \(\Delta{ABC}\) vuông tại \(C\), áp dụng định lí Pytago, ta có:
\(AB^2=CB^2+AC^2\)
\(\Leftrightarrow AB^2=0,9^2+1,2^2\)
\(\Leftrightarrow AB^2=0,81+1,44=2,25\)
\(\Leftrightarrow AB=\sqrt{2,25}=1,5m\)
Vì \(\Delta{ABC}\) vuông tại \(C\) nên góc \(B\) và \(A\) là hai góc phụ nhau. Do vậy, ta có:
\(\sin A=\cos B=\dfrac{BC}{AB}=\dfrac{1,2}{1,5}=\dfrac{4}{5}\)
\(\cos A=\sin B=\dfrac{AC}{AB} =\dfrac{0,9}{1,5}=\dfrac{3}{5}\)
\(\tan A=\cot B=\dfrac{BC}{AC}=\dfrac{1,2}{0,9}=\dfrac{4}{3}\)
\(\cot A=\tan B=\dfrac{AC}{BC}=\dfrac{0,9}{1,2}=\dfrac{3}{4}\)
Nhận xét: Với hai góc phụ nhau, ta có sin góc này bằng cosin góc kia, tan góc này bằng cotan góc kia.
Bình luận
Chia sẻ
- Bài 12 trang 76 SGK Toán 9 tập 1
- Bài 13 trang 77 SGK Toán 9 tập 1
- Bài 14 trang 77 SGK Toán 9 tập 1
- Bài 15 trang 77 SGK Toán 9 tập 1
- Bài 16 trang 77 SGK Toán 9 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
