Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 2. Tỉ số lượng giác của góc nhọn

Đề kiểm tra 15 phút - Đề số 4 - Bài 2 - Chương 1 - Hình học 9


Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 2 - Chương 1 - Hình học 9

Lựa chọn câu để xem lời giải nhanh hơn

Đề bài

Bài 1. Rút gọn biểu thức \(A = {\left( {\sin \alpha  + \cos \alpha } \right)^2} + {\left( {\sin \alpha  - \cos \alpha } \right)^2}\)

Bài 2. Cho \(∆ABC \) vuông tại A. Biết \(BC = a\), đường cao AH.

Chứng minh rằng:

\(AH = a.{\mathop{\rm sinBcosB}\nolimits} ;\)\(\,BH = a.co{s^2}B;CH = a.{\sin ^2}B\)

LG bài 1

Phương pháp giải:

Sử dụng: \(\sin^2\alpha +\cos^2 \alpha =1\)

Lời giải chi tiết:

\( A = {\left( {\sin \alpha  + \cos \alpha } \right)^2} + {\left( {\sin \alpha  - \cos \alpha } \right)^2}\)

\(= {\sin ^2}\alpha  + {\cos ^2}\alpha  + 2\sin \alpha \cos \alpha \)\(\;+ {\sin ^2}\alpha  + {\cos ^2}\alpha  - 2\sin \alpha \cos \alpha  \)

\(= {\sin ^2}\alpha  + {\cos ^2}\alpha  + {\sin ^2}\alpha  + {\cos ^2}\alpha  \)

\(  = 1 + 1 = 2\)

LG bài 2

Phương pháp giải:

Sử dụng \(\sin \alpha  = \dfrac{{cạnh\,đối}}{{cạnh\,huyền}};\cos \alpha  = \dfrac{{cạnh\,kề}}{{cạnh\,huyền}}\)

Lời giải chi tiết:

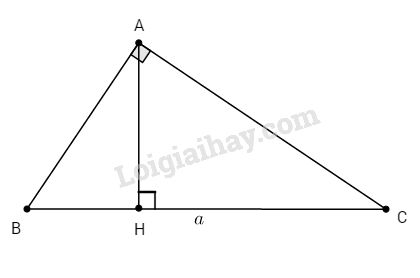
Ta có: \(∆AHB\) vuông tại H nên: 

\(\sin B = {{AH} \over {AB}} \Rightarrow AH = AB.\sin B\) (1)

Lại có: \(∆ABC\) vuông tại A, ta có:

\({\mathop{\rm cosB}\nolimits}  = {{AB} \over {BC}} \)

\(\Rightarrow AB = BC.\cos B = a.\cos B\) (2)

Thay (2) vào (1), ta có: \(AH = a.\sin B\cos B\)

Tương tự \(∆AHB\) vuông ta có:

\(\cos B = {{BH} \over {AB}} \Rightarrow BH = AB.\cos B\)   (3)

Thay (2) vào (3), ta có: \(BH = a.co{s^2}B\)

Ta có: \({\widehat A_1} = \widehat B\) (cùng phụ \(\widehat C\)). Xét tam giác vuông AHC có:

\(\sin {\widehat A_1}\,hay\,\sin B = {{CH} \over {AC}}\)

\(\Rightarrow CH = AC.{\mathop{\rm sinB}\nolimits} \) (4)

Lại có: \(\sin B = {{AC} \over {BC}}\)

\(\Rightarrow AC = BC.\sin B = a.\sin B\) (5)

Thay (5) vào (4), ta có: \(CH = a.{\sin ^2}B.\)

Loigiaihay.com


Bình chọn:
4.1 trên 9 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com. , cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua