Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Bài 3. Thể tích của hình hộp chữ nhật

Lý thuyết thể tích của hình hộp chữ nhật


A. KIẾN THỨC CƠ BẢN

I. Các kiến thức cần nhớ 

1. Đường thẳng vuông góc với mặt phẳng

- Nếu đường thẳng $\left( a \right)$ vuông góc với hai dường thẳng cắt nhau của mp $\left( P \right)$ thì đường thẳng  $\left( a \right)$ vuông góc với mp $\left( P \right).$

- Nếu đường thẳng $\left( a \right)$ vuông góc với mp $\left( P \right)$ tại điểm $I$  thì nó vuông góc với mọi đường thẳng đi qua $I$ và nằm trong mp $\left( P \right).$

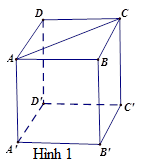
Trên hình 1, \(AA' \bot AB,AA' \bot AD\) nên \(AA' \bot mp(ABCD);AA' \bot AC\)

2. Mặt phẳng vuông góc với mặt phẳng

Nếu mp $\left( Q \right)$ chứa một đường thẳng vuông góc với mp $\left( P \right)$ thì mp $\left( Q \right)$ vuông góc với mp $\left( P \right).$

Trên hình 1, \(AA' \bot mp(ABCD)\) nên \((AA'B'B) \bot (ABCD)\)

3. Các công thức tính thể tích

Thể tích của hình hộp chữ nhật $V = abc$ ($a,b,c$ là các kích thước của hình hộp chữ nhật)

Thể tích của hình lập phương: $V = {a^3}$ ($a$  là cạnh của hình lập phương).

II. Các dạng toán thường gặp

Dạng 1: Sử dụng mối quan hệ vuông góc để xác định các đường thẳng và mặt phẳng vuông góc.

Phương pháp:

Sử dụng các kiến thức

- Nếu đường thẳng $\left( a \right)$ vuông góc với hai dường thẳng cắt nhau của mp $\left( P \right)$ thì đường thẳng  $\left( a \right)$ vuông góc với mp $\left( P \right).$

- Nếu đường thẳng $\left( a \right)$ vuông góc với mp $\left( P \right)$ tại điểm $I$  thì nó vuông góc với mọi đường thẳng đi qua $I$ và nằm trong mp $\left( P \right).$

- Nếu mp $\left( Q \right)$ chứa một đường thẳng vuông góc với mp $\left( P \right)$ thì mp $\left( Q \right)$ vuông góc với mp $\left( P \right).$

Dạng 2: Sử dụng các công thức tính thể tích để tính thê tích hình lập phương và hình hộp chữ nhật.

Phương pháp:

Ta sử dụng các công thức sau:

-Thể tích của hình hộp chữ nhật $V = abc$ ($a,b,c$ là các kích thước của hình hộp chữ nhật)

- Thể tích của hình lập phương: $V = {a^3}$ ($a$  là cạnh của hình lập phương).

Dạng 3: Các dạng khác

Phương pháp:

Ta sử dụng các công thức tính diện tich hình vuông, hình chữ nhật, định lý Pytago và các kiến thức về hình hộp chữ nhật, hình lập phương để tính toán.


Bình chọn:
4.1 trên 29 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store