 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Bài 3. Thể tích của hình hộp chữ nhật
Bài 3. Thể tích của hình hộp chữ nhật
Bài 12 trang 104 SGK Toán 8 tập 2
A, B, C và D là những đỉnh của hình hộp chữ nhật
Đề bài
\(A,\, B,\, C \) và \(D\) là những đỉnh của hình hộp chữ nhật cho ở hình 88.
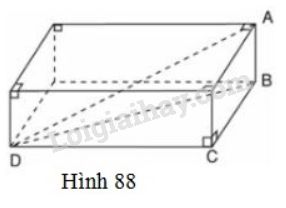
Hãy điền số thích hợp vào các ô trống ở bảng sau:
|
AB |
6 |
13 |
14 |
|
|
BC |
15 |
16 |
|
34 |
|
CD |
42 |
|
70 |
62 |
|
DA |
|
45 |
75 |
75 |
Kết quả bài 12 minh họa công thức quan trọng sau:
\(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Áp dụng định lý Py-ta-go trong tam giác vuông để chứng minh công thức:
\(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)
- Áp dụng công thức bên trên để tìm độ dài các đoạn thẳng chưa biết.
Lời giải chi tiết
Trước hết ta chứng minh hệ thức sau: \(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)
Ta có : \( \triangle BCD\) vuông tại \( C \Rightarrow BD^2 = DC^2 + BC^2\)
\( \triangle ABD\) vuông tại \(B \Rightarrow AD^2 = BD^2 + AB^2\)
\( \Rightarrow AD^2 = DC^2 +BC^2 + AB^2 \)
Suy ra: \(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)
Áp dụng hệ thức này ta sẽ tính được độ dài một cạnh khi biết ba độ dài kia.
Cột 1: \(AB=6,BC=15, CD=42\)
\(DA = \sqrt {{6^2} + {{15}^2} + {{42}^2}} = \sqrt {2025} \)\(\,= 45\)
Cột 2: \(AB=13,BC=16,DA=45\)
\(\eqalign{
& D{A^2} = A{B^2} + B{C^2} + C{D^2} \cr
& \Rightarrow C{D^2} = D{A^2} - A{B^2} - B{C^2} \cr
& \Rightarrow CD = \sqrt {D{A^2} - A{B^2} - B{C^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{45}^2} - {{16}^2} - {{13}^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {1600} = 40 \cr} \)
Cột 3: \(AB=14,CD=70,DA=75\)
\(\eqalign{
& D{A^2} = A{B^2} + B{C^2} + C{D^2} \cr
& \Rightarrow B{C^2} = D{A^2} - A{B^2} - C{D^2} \cr
& \Rightarrow BC = \sqrt {D{A^2} - A{B^2} - C{D^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{75}^2} - {{14}^2} - {{70}^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {529} = 23 \cr} \)
Cột 4: \(BC=34,CD=62,DA=75\)
\(\eqalign{
& D{A^2} = A{B^2} + B{C^2} + C{D^2} \cr
& \Rightarrow A{B^2} = D{A^2} - B{C^2} - C{D^2} \cr
& \Rightarrow AB = \sqrt {D{A^2} - B{C^2} - C{D^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{75}^2} - {{34}^2} - {{62}^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {625} = 25 \cr} \)
Do đó ta có kết quả như bảng dưới đây:
|
AB |
6 |
13 |
14 |
25 |
|
BC |
15 |
16 |
23 |
34 |
|
CD |
42 |
40 |
70 |
62 |
|
DA |
45 |
45 |
75 |
75 |
Loigiaihay.com












Danh sách bình luận