Đề số 20 - Đề kiểm tra học kì 1 - Toán 9

Đề bài

Câu 1 (2,5 điểm): Cho hai biểu thức: $A\, = \,\dfrac{{2\sqrt x  - 4}}{{\sqrt x  - 1}}$ và $B\, = \,\dfrac{{\sqrt x }}{{\sqrt x  - 1}} + \dfrac{3}{{\sqrt x  + 1}} - \dfrac{{6\sqrt x  - 4}}{{x - 1}}$ với $x \ge 0,\,\,x \ne 1.$

1. Tính giá trị của A khi $x = 4.$

2. Rút gọn B.

3. So sánh A.B với 5.  

Câu 2 (2,0 điểm):

1. Thực hiện phép tính: $\left( {3\sqrt 8  - \sqrt {18}  + 5\sqrt {\dfrac{1}{2}}  + \sqrt {50} } \right).3\sqrt 2 .$

2. Giải phương trình: $\sqrt {4{x^2} - 4x + 1}  - 5 = 2.$

Câu 3 (1,5 điểm): Cho hàm số $y = 3x + 2$ có đồ thị là đường thẳng $\left( {{d_1}} \right).$

1. Điểm $A\left( {\dfrac{1}{3};3} \right)$ có thuộc đường thẳng $\left( {{d_1}} \right)$ không? Vì sao?

2. Tìm giá trị của $m$ để đường thẳng $\left( {{d_1}} \right)$ và đường thẳng $\left( {{d_2}} \right)$ có phương trình $y =  - 2x - m$ cắt nhau tại điểm có hoành độ bằng 1.

Câu 4 (3,5 điểm): Cho đường tròn $\left( {O;R} \right)$ đường kính AB và điểm C bất kỳ thuốc đường tròn (C khác A và B). Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BC ở D. Đường thẳng tiếp xúc với đường tròn tại C cắt AD ở E.

1. Chứng minh bốn điểm A,E,C,O cùng thuộc một đường tròn.

2. Chứng minh $BC.BD = 4{R^2}$ và OE song song với BD.

3. Đường thẳng kẻ qua O và vuông góc với BC tại N cắt tia EC ở F. Chứng minh BF là tiếp tuyến của đường tròn $\left( {O;R} \right)$

4. Gọi H là hình chiếu của C trên AB, M là giao của AC và OE. Chứng minh rằng khi điểm C di động trên đường tròn $\left( {O;R} \right)$ và thỏa mãn yêu cầu đề bài thì đường tròn ngoại tiếp tam giác HMN luôn đi qua một điểm cố định.

Câu 5 (0,5 điểm):

Tìm giá trị nhỏ nhất của biểu thức $P = x + \dfrac{9}{{x - 2}} + 2010$ với $x > 2.$

LG bài 1

Lời giải chi tiết:

1. Tính giá trị của A khi $x = 4.$

Khi $x = 4$ thì $A\, = \,\dfrac{{2\sqrt 4  - 4}}{{\sqrt 4  - 1}} = \dfrac{{2.2 - 4}}{{2 - 1}} = \dfrac{0}{1} = 0$

2. Rút gọn B.

$\begin{array}{l}B\, = \,\dfrac{{\sqrt x }}{{\sqrt x  - 1}} + \dfrac{3}{{\sqrt x  + 1}} - \dfrac{{6\sqrt x  - 4}}{{x - 1}}\\\;\;\; = \dfrac{{\sqrt x \left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} + \dfrac{{3\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}} - \dfrac{{6\sqrt x  - 4}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\\,\,\,\, = \dfrac{{x + \sqrt x  + 3\sqrt x  - 3 - 6\sqrt x  + 4}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} = \dfrac{{x - 2\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\\,\,\,\, = \dfrac{{{{\left( {\sqrt x  - 1} \right)}^2}}}{{x - 1}} = \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}}.\end{array}$

3. So sánh A.B với 5. 

$\begin{array}{l}A.B - 5 = \dfrac{{2\sqrt x  - 4}}{{\sqrt x  - 1}}.\dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}} - 5 = \dfrac{{2\sqrt x  - 4}}{{\sqrt x  + 1}} - 5\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{2\sqrt x  - 4 - 5\sqrt x  - 5}}{{\sqrt x  + 1}} = \dfrac{{ - 3\sqrt x  - 9}}{{\sqrt x  + 1}}\end{array}$

Có $\sqrt x  \ge 0\;\forall x \ge 0 \Rightarrow  - 3\sqrt x  \le 0\;\forall x \ge 0 \Rightarrow  - 3\sqrt x  - 9 < 0\;\forall x \ge 0$  

Mặt khác  $\sqrt x  \ge 0\;\forall x \ge 0 \Rightarrow \sqrt x  + 1 > 0\;\forall x \ge 0.$

$\Rightarrow A.B - 5 = \dfrac{{ - 3\sqrt x  - 9}}{{\sqrt x  + 1}} < 0\;\;\forall x \ge 0 \Rightarrow \,A.B < 5$

LG bài 2

Lời giải chi tiết:

1. Thực hiện phép tính: $\left( {3\sqrt 8  - \sqrt {18}  + 5\sqrt {\dfrac{1}{2}}  + \sqrt {50} } \right).3\sqrt 2 .$

$\begin{array}{l}\left( {3\sqrt 8  - \sqrt {18}  + 5\sqrt {\dfrac{1}{2}}  + \sqrt {50} } \right).3\sqrt 2\\  = \left( {3.2\sqrt 2  - 3\sqrt 2  + \dfrac{{5\sqrt 2 }}{2} + 5\sqrt 2 } \right).3\sqrt 2 \\= \dfrac{{21\sqrt 2 }}{2}.3\sqrt 2\\  = 21.3 = 63.\end{array}$

2. Giải phương trình: $\sqrt {4{x^2} - 4x + 1}  - 5 = 2.$

Điều kiện: $4{x^2} - 4x + 1 \ge 0 \Leftrightarrow {\left( {2x - 1} \right)^2} \ge 0$ luôn đúng với mọi $x$

 $\sqrt {4{x^2} - 4x + 1}  - 5 = 2$

$\Leftrightarrow \sqrt {{{\left( {2x - 1} \right)}^2}}  = 7$

$\Leftrightarrow \left| {2x - 1} \right| = 7$

$\Leftrightarrow \left[ \begin{array}{l}2x - 1 = 7\\2x - 1 =  - 7\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\x =  - 3\end{array} \right.$

Vậy phương trình có tập nghiệm $S = \left\{ { - 3;\;4} \right\}.$  

LG bài 3

Lời giải chi tiết:

1. Điểm $A\left( {\dfrac{1}{3};3} \right)$ có thuộc đường thẳng $\left( {{d_1}} \right)$ không? Vì sao?

 Thay tọa độ điểm A vào công thức hàm số ta có: $3.\dfrac{1}{3} + 2 = 1 + 2 = 3$ .

Vậy $A\left( {\dfrac{1}{3};3} \right)$ thuộc đường thẳng $\left( {{d_1}} \right):y = 3x + 2$

2. Tìm giá trị của $m$ để đường thẳng $\left( {{d_1}} \right)$ và đường thẳng $\left( {{d_2}} \right)$ có phương trình $y =  - 2x - m$ cắt nhau tại điểm có hoành độ bằng 1.

Phương trình hoành độ giao điểm của $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right)$ là: $3x + 2 =  - 2x - m \Leftrightarrow m =  - 5x - 2$  $\left( 1 \right)$

Vì $\left( {{d_1}} \right)$ cắt $\left( {{d_2}} \right)$ tại điểm có hoành độ bằng 1 nên $x = 1$ là nghiệm của phương trình $\left( 1 \right)$

$\; \Rightarrow m =  - 5.1 - 2 =  - 7$

Vậy với $m =  - 7$  thỏa mãn yêu cầu để bài.

LG bài 4

Lời giải chi tiết:

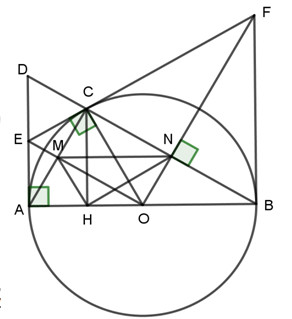
1. Chứng minh bốn điểm A, E, C, O cùng thuộc một đường tròn.

AE là tiếp tuyến tại A của $\left( {O;R} \right) \Rightarrow \angle EAO = {90^o}$

CE là tiếp tuyến tại C của $\left( {O;R} \right) \Rightarrow \angle ECO = {90^o}$

$\Rightarrow$ C, A cùng thuộc đường tròn đường kính OE

$\Rightarrow$ A, E, C, O cùng thuộc đường tròn đường kính OE

2. Chứng minh $BC.BD = 4{R^2}$ và OE song song với BD.

Ta có điểm C thuộc $\left( O \right)$ đường kính $AB = 2R$

$\Rightarrow$$\angle ACB = {90^o} \Rightarrow AC \bot BD$

$\Rightarrow$ AC là đường cao trong $\Delta ABD$

 Xét $\Delta ABD$ vuông tại A đường cao AC ta có:

$BC.BD = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}$

Ta có AE là tiếp tuyến tại A của $\left( {O;R} \right)$

         CE là tiếp tuyến tại C của $\left( {O;R} \right)$

         $AE \cap CE = \left\{ E \right\}$

$\Rightarrow$ $OE \bot AC$ (tính chất hai tiếp tuyến cắt nhau)

Mà $BD \bot AC$ (chứng minh trên) $\Rightarrow$ $OE\parallel BD$ (từ vuông góc đến song song)

3. Đường thẳng kẻ qua O và vuông góc với BC tại N cắt tia EC ở F. Chứng minh BF là tiếp tuyến của đường tròn $\left( {O;R} \right)$

Ta có $OF \bot BC$ tại N (gt) $\Rightarrow$$\angle BOF = \angle COF = \dfrac{1}{2}\angle BOC$ (đường cao đồng thời là đường trung tuyến trong tam giác cân)

Mặt khác $\angle BCF = \dfrac{1}{2}\angle BOC$ (CF là tiếp của $\left( O \right)$ tại C)

$\Rightarrow \angle BOF = \angle BCF\left( { = \dfrac{1}{2}\angle BOC} \right)$ $\Rightarrow$ BOCF là tứ giác nội tiếp

$\Rightarrow \angle OBF + \angle OCF = {180^o} \Leftrightarrow \angle OBF + {90^o} = {180^o}$  ($\angle OCF = {90^o}$ do CF là tiếp tuyến của $\left( O \right)$ tại C)

$\Rightarrow \angle OBF = {90^o} \Rightarrow BF$  là tiếp tuyến của $\left( {O;R} \right)$

4. Gọi  H  là hình chiếu của C trên AB, M  là giao của AC và OE. Chứng minh rằng khi điểm C di động trên đường tròn $\left( {O;R} \right)$ và thỏa mãn yêu cầu đề bài thì đường tròn ngoại tiếp tam giác HMN luôn đi qua một điểm cố định.

Ta có $OE\parallel CA$ (chứng minh trên) $\Rightarrow \angle OMC = {90^o}$

Mặt khác $\angle MCN = \angle ONC = {90^o}$ $\Rightarrow \,OMCN$ là hình chữ nhật $\Rightarrow$ $\angle OMN = \angle OCN$ (hai góc nội tiếp cùng chắn cung $ON$)

Ta có $\angle OHC = \angle ONC = {90^o}$ $\Rightarrow$ OHCN là tứ giác nội tiếp $\Rightarrow$ $\angle OHN = \angle OCN$ (hai góc nội tiếp cùng chắn cung $ON$)

$\Rightarrow \angle OMN = \angle OHN\left( { = \angle OCN} \right)$

$\Rightarrow$ HMNO là tứ giác nội tiếp (dhnb)

$\Rightarrow$ Đường tròn ngoại tiếp tam giác HMN luôn đi qua O là điểm cố định. (đpcm)

LG bài 5

Lời giải chi tiết:

Tìm giá trị nhỏ nhất của biểu thức $P = x + \dfrac{9}{{x - 2}} + 2010$ với $x > 2.$

$P = x + \dfrac{9}{{x - 2}} + 2010 = x - 2 + \dfrac{9}{{x - 2}} + 2012$

Với $x > 2 \Leftrightarrow x - 2 > 0 \Rightarrow \dfrac{9}{{x - 2}} > 0$

Áp dụng bất đẳng thức Cô-si cho hai số không âm $x - 2$ và $\dfrac{9}{{x - 2}}$

$\begin{array}{l}x - 2 + \dfrac{9}{{x - 2}} \ge 2.\sqrt {\left( {x - 2} \right).\dfrac{9}{{x - 2}}}  = 2\sqrt 9  = 6\\ \Rightarrow \,P = x - 2 + \dfrac{9}{{x - 2}} + 2012 \ge 6 + 2012 = 2018\end{array}$

Dấu “=” xảy ra khi $x - 2 = \dfrac{9}{{x - 2}}$

$\Leftrightarrow {\left( {x - 2} \right)^2} = 9$

$\Leftrightarrow \left[ \begin{array}{l}x - 2 = 3\\x - 2 =  - 3\end{array} \right.$

$\Leftrightarrow \left[ \begin{array}{l}x = 5\\x =  - 1\end{array} \right.$

$\Leftrightarrow x = 5$ (do $x > 2$)

Vậy giá trị nhỏ nhất của P là 2018 tại $x = 5$.

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 9 tại Tuyensinh247.com

 Loigiaihay.com