Đề thi toán 9, đề kiểm tra toán 9 có đáp án và lời giải chi tiết Đề ôn tập học kì 1 – Có đáp án và lời giải

Đề kiểm tra học kì 1 Toán 9 - Đề số 24


Đáp án và lời giải chi tiết Đề số 24 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9

Lựa chọn câu để xem lời giải nhanh hơn

Đề bài

Câu 1: (2 điểm) Tính:

a) \(\sqrt {50}  - 3\sqrt {72}  + 4\sqrt {128}  - 2\sqrt {162} \)

b)\(\sqrt {9 - 4\sqrt 5 }  + \sqrt {14 - 6\sqrt 5 } \)

Câu 2: (1,5 điểm) Cho hàm số\(y =  - 3x + 1\)có đồ thị (d1) và hàm số \(y = x - 3\)có đồ thị (d2).

a) Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ.        

b) Tìm tọa độ giao điểm của (d1) và (d2) bằng phép toán.

Câu 3: (1 điểm) Giải phương trình: \(\sqrt {9x - 45}  + \sqrt {4x - 20}  = 15\)

Câu 4: (1 điểm) Một chiếc máy bay xuất phát từ vị trí A bay lên với vận tốc 500 km/h theo đường thẳng tạo với phương ngang một góc nâng 200 (xem hình bên).

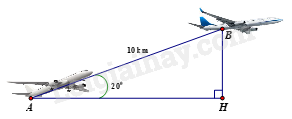
Nếu máy bay chuyển động theo hướng đó đi được 10 km đến vị trí B thì mất mấy phút?(làm tròn đến phần chục). Khi đó máy bay sẽ ở độ cao bao nhiêu kilômét so với mặt đất (BH là độ cao)? (độ cao làm tròn đến hàng đơn vị)

Câu 5: (1 điểm) Do hoạt động công nghiệp thiếu kiểm soát của con người làm cho nhiệt độ trái đất tăng dần một cách rất đáng ngại. Các nhà khoa học cảnh báo và đưa ra công thức dự báo nhiệt độ trung bình trên bề mặt trái đất như sau: T = 0,02t + 15; trong đó T là nhiệt độ trung bình của bề mặt trái đất tính theo độ C; t là số năm kể từ năm 1950.

a) Em hãy cho biết nhiệt độ trung bình của bề mặt trái đất năm 1950.

b) Em hãy tính xem nhiệt độ trung bình của bề mặt trái đất vào năm 2050 là bao nhiêu?

Câu 6: (0,5 điểm) Ông A mua 300 cái cặp với giá một cái cặp là 100 000 ngàn đồng. Ông bán 200 cái cặp mỗi cái so với giá vốn ông lãi được 30% với 50 cái còn lại mỗi cái ông lãi 10% và 50 cái cuối mỗi cái ông bán lỗ vốn 5%. Hỏi sau khi bán xong số cặp trên ông A lời hay lỗ bao nhiêu tiền?

Câu 7: (3 điểm) Từ điểm A nằm ngoài đường tròn (O;R) kẻ 2 tiếp tuyến AB và AC (B, C là tiếp điểm) xuống đường tròn. Gọi H là giao điểm của BC và OA.

a) Chứng minh: OA vuông góc với BC ?

b) Kẻ đường kính BD của (O), gọi E là giao điểm thứ 2 của AD với (O). Chứng minh: AD.AE = AH.AO ?

c) Chứng minh: \(\sqrt {ED.EA}  = \frac{{AG}}{{\cot \widehat {BAD} + \cot \widehat {BGA}}}\)

-------- Hết --------

Lời giải

Câu 1: (2 điểm) Tính:

a) \(\sqrt {50}  - 3\sqrt {72}  + 4\sqrt {128}  - 2\sqrt {162} \)

b)\(\sqrt {9 - 4\sqrt 5 }  + \sqrt {14 - 6\sqrt 5 } \)

Phương pháp

Sử dụng công thức khai phương căn bậc hai.

Lời giải

a) \(\sqrt {50}  - 3\sqrt {72}  + 4\sqrt {128}  - 2\sqrt {162} \)

\( = 5\sqrt 2  - 18\sqrt 2  + 32\sqrt 2  - 18\sqrt 2 \)

\( = \sqrt 2 \)                                                       

b)\(\sqrt {9 - 4\sqrt 5 }  + \sqrt {14 - 6\sqrt 5 } \)

\( = \sqrt {{{\left( {\sqrt 5  - 2} \right)}^2}}  + \sqrt {{{\left( {3 - \sqrt 5 } \right)}^2}} \)

\( = 1\)                       

Câu 2: (1,5 điểm) Cho hàm số\(y =  - 3x + 1\)có đồ thị (d1) và hàm số \(y = x - 3\)có đồ thị (d2).

a) Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ.        

b) Tìm tọa độ giao điểm của (d1) và (d2) bằng phép toán.

Phương pháp

a) Lấy hai điểm thuộc đồ thị hàm số, ta được đồ thị của hàm số đó.

b) Viết phương trình hoành độ giao điểm của (d1) và (d2). Tìm nghiệm của phương trình. Thay giá trị x tìm được để tìm y.

Lời giải

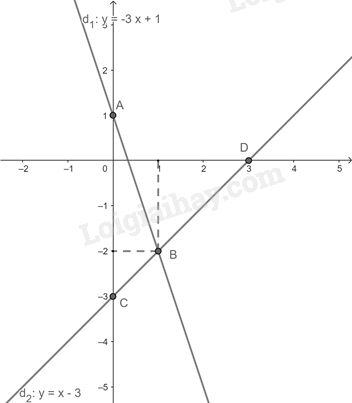
a) Ta thấy:

+) \(A\left( {0;1} \right),B\left( {1; - 2} \right)\) thuộc đồ thị hàm số \(y =  - 3x + 1\).

+) \(C\left( {0; - 3} \right);D\left( {3;0} \right)\) thuộc đồ thị hàm số \(y = x - 3\).

Từ đó ta có đồ thị của hai hàm số:

 

b) Ta có phương trình hoành độ giao điểm của hai đường thẳng (d1) và (d2) là:

\(\begin{array}{l} - 3x + 1 = x - 3\\ - 3x - x =  - 3 - 1\\ - 4x =  - 4\\x = 1\end{array}\)

Với x = 1 ta có \(y = 1 - 3 =  - 2\) ta được điểm \(B\left( {1; - 2} \right)\).

Vậy giao điểm của (d1) và (d2) là điểm \(B\left( {1; - 2} \right)\).

Câu 3: (1 điểm) Giải phương trình: \(\sqrt {9x - 45}  + \sqrt {4x - 20}  = 15\)

Phương pháp

Sử dụng công thức khai phương căn bậc hai để có nhân tử chung.

Lời giải

\(\sqrt {9x - 45}  + \sqrt {4x - 20}  = 15\)

\( \Leftrightarrow \sqrt {9(x - 5)}  + \sqrt {4(x - 5)}  = 15\) (ĐK: \(x \ge 5\))

\( \Leftrightarrow 3\sqrt {x - 5}  + 2\sqrt {x - 5}  = 15\)

\( \Leftrightarrow \sqrt {x - 5}  = 3\)

\( \Leftrightarrow \sqrt {x\,\, - \,\,3} \,\, = \,\,\frac{5}{3}\,\,\)

\( \Leftrightarrow x = 14\,\)(TM)

Vậy nghiệm của phương trình là \(x = 14\,\).

Câu 4: (1 điểm) Một chiếc máy bay xuất phát từ vị trí A bay lên với vận tốc 500 km/h theo đường thẳng tạo với phương ngang một góc nâng 200 (xem hình bên).

Nếu máy bay chuyển động theo hướng đó đi được 10 km đến vị trí B thì mất mấy phút?(làm tròn đến phần chục). Khi đó máy bay sẽ ở độ cao bao nhiêu kilômét so với mặt đất (BH là độ cao)? (độ cao làm tròn đến hàng đơn vị)

Phương pháp

Sử dụng tỉ số lượng giác của góc nhọn.

Lời giải

Thời gian máy bay chuyển động theo hướng đó đi được 10 km đến vị trí B là:

10 : 500 = 0,02 (giờ) = 1,2 (phút)                                                                                                     

Xét \(\Delta \)ABH vuông tại H, ta có :

 \(\sin A = \frac{{BH}}{{AB}}\)\( \Rightarrow \sin {20^0} = \frac{{BH}}{{10}}\)\( \Rightarrow BH = 10.\sin {20^0} \approx 3\left( {km} \right)\)

Vậy máy bay sẽ ở độ cao 3km  so với mặt đất.      

Câu 5: (1 điểm) Do hoạt động công nghiệp thiếu kiểm soát của con người làm cho nhiệt độ trái đất tăng dần một cách rất đáng ngại. Các nhà khoa học cảnh báo và đưa ra công thức dự báo nhiệt độ trung bình trên bề mặt trái đất như sau: T = 0,02t + 15; trong đó T là nhiệt độ trung bình của bề mặt trái đất tính theo độ C; t là số năm kể từ năm 1950.

a) Em hãy cho biết nhiệt độ trung bình của bề mặt trái đất năm 1950.

b) Em hãy tính xem nhiệt độ trung bình của bề mặt trái đất vào năm 2050 là bao nhiêu?

Phương pháp

a) Năm 1950 thì t = 1950 – 1950, thay t vào T = 0,02t + 15 để tính nhiệt độ trung bình.

b) Năm 2050 thì t = 2050 – 1950, thay t vào T = 0,02t + 15 để tính nhiệt độ trung bình.

Lời giải

a) Năm 1950 thì t = 1950 – 1950 = 0, thay t = 0 vào T = 0,02.0 + 15 = 15 (0C)

b) Năm 2050 thì t = 2050 – 1950 = 100, thay t = 100 vào T = 0,02.100 + 15 = 17 (0C)

Câu 6: (0,5 điểm) Ông A mua 300 cái cặp với giá một cái cặp là 100 000 ngàn đồng. Ông bán 200 cái cặp mỗi cái so với giá vốn ông lãi được 30% với 50 cái còn lại mỗi cái ông lãi 10% và 50 cái cuối mỗi cái ông bán lỗ vốn 5%. Hỏi sau khi bán xong số cặp trên ông A lời hay lỗ bao nhiêu tiền?

Phương pháp

Tính số tiền ông A mua 300 cái cặp.

Tính số tiền ông A bán 200 cái cặp, 50 cái tiếp theo và 50 cái cuối.

Lấy tổng số tiền đó trừ đi số tiền ông A mua để xem ông A lời hay lỗ bao nhiêu tiền.

Lời giải

Số tiền ông A mua 300 cái cặp là:

300 . 100 000 = 30 000 000 (đồng).

Số tiền ông A bán 200 cái cặp là:

200. 100 000. (100% + 30%) = 26 000 000 (đồng)

Số tiền ông A bán 50 cái tiếp theo là:

50. 100 000. (100% + 10%) = 5 500 000 (đồng)

Số tiền ông A bán 50 cái cuối là:

50. 100 000. (100% - 5%) = 4 750 000 (đồng)

Vậy tổng số tiền ông A bán cặp là:

26 000 000 + 5 500 000 + 4 750 000 = 36 250 000 (đồng)

Ta có: 36 250 000 - 30 000 000 = 6 250 000

Vậy ông A lời được 6 250 000 đồng.

Câu 7: (3 điểm) Từ điểm A nằm ngoài đường tròn (O;R) kẻ 2 tiếp tuyến AB và AC (B, C là tiếp điểm) xuống đường tròn. Gọi H là giao điểm của BC và OA.

a) Chứng minh: OA vuông góc với BC ?

b) Kẻ đường kính BD của (O), gọi E là giao điểm thứ 2 của AD với (O). Chứng minh: AD.AE = AH.AO ?

c) Chứng minh: \(\sqrt {ED.EA}  = \frac{{AG}}{{\cot \widehat {BAD} + \cot \widehat {BGA}}}\)

Phương pháp

a) Ta có : AB = AC ; OB = OC
Suy ra OA là đường trung trực của BC
Suy ra OA vuông góc BC

b) Chứng minh : $\Delta AEC\backsim \Delta ACD$
Suy ra AC2 = AE.AD
Mặc khác AC2 = AH.AO
Suy ra AE.AD = AH.AO

c) Chứng minh : \(BE.\left( {cot\widehat {BGA} + cot\widehat {BAD}} \right) = AG\)
Suy ra \(\sqrt {ED.EA}  = \frac{{AG}}{{\cot \widehat {BGA} + \cot \widehat {BAD}}}\)

Lời giải

 

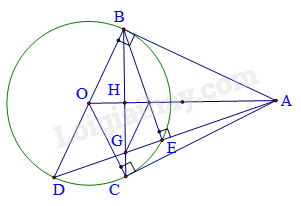
a) Vì (O; R) có hai tiếp tuyến AB, AC => AB = AC => A thuộc đường trung trực của BC.

Vì \(B,C \in \left( O \right)\) suy ra OB = OC. => O thuộc đường trung trực của BC.

Suy ra OA là đường trung trực của BC => OA \( \bot \) BC.

b) Xét (O) có \(\widehat {ACE}\) và \(\widehat {CDA}\) cùng chắn cung EC \( \Rightarrow \widehat {ACE} = \widehat {CDA}\).

Xét tam giác AEC và tam giác ACD có:

\(\widehat {EAC}\) chung

\(\widehat {ACE} = \widehat {CDA}\)

\(\begin{array}{l} \Rightarrow \Delta AEC\backsim \Delta ACD \\ \Rightarrow \frac{AE}{AC}=\frac{AC}{AD} \\ \Rightarrow AE.AD=A{{C}^{2}} \end{array}\)

Xét tam giác vuông OAC có đường cao CH \( \Rightarrow A{C^2} = AH.AO\)

\( \Rightarrow AE.AD = AH.AO\)

c) Ta có cot\(\widehat {BGA}\) = cot\(\widehat {BGE}\)= \(\frac{{GE}}{{BE}}\)

cot\(\widehat {BAD}\) = cot\(\widehat {BAE}\)= \(\frac{{AE}}{{BE}}\)

\( \Rightarrow \cot \widehat {BGA} + \cot \widehat {BAD} = \frac{{GE}}{{BE}} + \frac{{AE}}{{BE}} = \frac{{AG}}{{BE}}\)

\(\begin{array}{l} \Rightarrow BE\left( {\cot \widehat {BGA} + \cot \widehat {BAD}} \right) = AG\\ \Rightarrow BE = \frac{{AG}}{{\cot \widehat {BGA} + \cot \widehat {BAD}}}\end{array}\)

Xét tam giác vuông ABD có đường cao BE \( \Rightarrow B{E^2} = ED.EA \Rightarrow BE = \sqrt {ED.EA} \)

Suy ra \(\sqrt {ED.EA}  = \frac{{AG}}{{\cot \widehat {BGA} + \cot \widehat {BAD}}}\)


Bình chọn:
4.9 trên 7 phiếu
Tải về đề thi và đáp án Tải về đề thi Tải về đáp án
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store