Đề kiểm tra giữa kì 1 Toán 9 - Đề số 13 có lời giải chi tiết
Đề kiểm tra giữa kì 1 Toán 9 - Đề số 13 có lời giải chi tiết
Đề bài
Phần I: Trắc nghiệm (3 điểm).
Câu 1: Giá trị của biểu thức \(P = \sqrt 5 \cdot \sqrt {20} \) là
A. 10 .
B. 5 .
C. 6 .
D. 8 .
Câu 2: Nghiệm của phương trình \(\sqrt x - 1 = 3\) là
A. 8 .
B. 9 .
C. 16 .
D. 11 .
Câu 3: Rút gọn biểu thức \(\frac{2}{{\sqrt 3 - 1}} - \frac{2}{{\sqrt 3 + 1}}\) thu được kết quả là
A. 0 .
B. 2 .
C. \(2\sqrt 3 \).
D. \( - 2\sqrt 3 \).
Câu 4: Điều kiện xác định của \(\sqrt {2022 - 2023x} \) là
A. \(x \ge \frac{{2022}}{{2023}}\).
B. \(x \le \frac{{2022}}{{2023}}\).
C. \(x \ge \frac{{2023}}{{2022}}\).
D. \(x \le \frac{{2023}}{{2022}}\).
Câu 5: Cho \(\Delta ABC\) vuông tại \({\rm{A}}\) có \(AB = 6\;{\rm{cm}},AC = 8\;{\rm{cm}}\). Độ dài đường cao \({\rm{AH}}\) bằng
A. \(\frac{5}{{24}}\;{\rm{cm}}\).
B. \(4,8\;{\rm{cm}}\).
C. \(23,04\;{\rm{cm}}\).
D. \(10\;{\rm{cm}}\).
Câu 6: Cho \(\Delta ABC\) vuông tại \({\rm{A}}\), có \(AB = 3,AC = 4\). Khi đó tanB bằng
A. \(\frac{3}{4}\).
B. \(\frac{3}{5}\).
C. \(\frac{4}{3}\).
D. \(\frac{4}{5}\).
Phần II. Tự luận (7 điểm):
Câu 7: (1,5d) Thực hiện phép tính:
a) \((3\sqrt 5 - 2\sqrt 3 ) \cdot \sqrt 5 + \sqrt {60} \).
b) \(\sqrt {125} - 4\sqrt {45} + 3\sqrt {20} + \sqrt {80} \).
Câu 8: (1,5đ) Giải phương trình:
a) \(\sqrt {4x + 20} + \sqrt {x + 5} - \frac{1}{3}\sqrt {9x + 45} = 4\);
b) \(\frac{{2\sqrt x - 7}}{3} + \sqrt x - \frac{{3\sqrt x - 5}}{2} = 1\)
Câu 9: (2đ) Cho biểu thức \(A = \frac{{{a^2} + \sqrt a }}{{a - \sqrt a + 1}} - \frac{{2a + \sqrt a }}{{\sqrt a }} + 1\) với \({\rm{a}} > 0\),
a) Rút gọn biểu thức \({\rm{A}}\).
b) Tìm \({\rm{a}}\) để \({\rm{A}} = 2\).
c) Tìm a để \({\rm{A}}\) đạt giá trị nhỏ nhất.
Câu 10: (2đ) Cho \(\Delta ABC\) vuông tại A có \(\widehat B = {30^0},AB = 6\;{\rm{cm}}\).
a) Giải \(\Delta ABC\).
b) Vẽ đường cao \({\rm{AH}}\) và trung tuyến \({\rm{AM}}\) của \(\Delta ABC\). Tính diện tích \(\Delta AHM\).
-------- Hết --------
Lời giải chi tiết
Phần I: Trắc nghiệm
|
1.A |
2.C |
3.B |
4.B |
5.B |
6.C |
Câu 1: Giá trị của biểu thức \(P = \sqrt 5 \cdot \sqrt {20} \) là
A. 10 .
B. 5 .
C. 6 .
D. 8 .
Phương pháp:
Công thức khai phương căn bậc hai, trục căn thức.
Lời giải:
\(P = \sqrt 5 .\sqrt {20} = \sqrt {5.20} = \sqrt {100} = 10\)
Đáp án A.
Câu 2: Nghiệm của phương trình \(\sqrt x - 1 = 3\) là
A. 8 .
B. 9 .
C. 16 .
D. 11 .
Phương pháp:
Bình phương 2 vế
Lời giải:
$\begin{align} \sqrt{x}-1=3\left( K:x\ge 0 \right) \\\Leftrightarrow \sqrt{x}=4\Leftrightarrow x=16 \\ \end{align}$
Đáp án C.
Câu 3: Rút gọn biểu thức \(\frac{2}{{\sqrt 3 - 1}} - \frac{2}{{\sqrt 3 + 1}}\) thu được kết quả là
A. 0 .
B. 2 .
C. \(2\sqrt 3 \).
D. \( - 2\sqrt 3 \).
Phương pháp:
Trục căn thức và rút gọn.
Lời giải:
\(\frac{2}{{\sqrt 3 - 1}} - \frac{2}{{\sqrt 3 + 1}} = \frac{{2\left( {\sqrt 3 + 1} \right) - 2\left( {\sqrt 3 - 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}} = \frac{4}{{3 - 1}} = 2\)
Đáp án B.
Câu 4: Điều kiện xác định của \(\sqrt {2022 - 2023x} \) là
A. \(x \ge \frac{{2022}}{{2023}}\).
B. \(x \le \frac{{2022}}{{2023}}\).
C. \(x \ge \frac{{2023}}{{2022}}\).
D. \(x \le \frac{{2023}}{{2022}}\).
Phương pháp:
\(\sqrt A \) xác định khi \(A \ge 0\)
Lời giải:
\(\sqrt {2022 - 2023x} \) xác định khi \(2022 - 2023x \ge 0 \Leftrightarrow x \le \frac{{2022}}{{2023}}\)
Đáp án B.
Câu 5: Cho \(\Delta ABC\) vuông tại \({\rm{A}}\) có \(AB = 6\;{\rm{cm}},AC = 8\;{\rm{cm}}\). Độ dài đường cao \({\rm{AH}}\) bằng
A. \(\frac{5}{{24}}\;{\rm{cm}}\).
B. \(4,8\;{\rm{cm}}\).
C. \(23,04\;{\rm{cm}}\).
D. \(10\;{\rm{cm}}\).
Phương pháp:
Áp dụng hệ thức lượng trong tam giác vuông
Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông cho tam giác ABC vuông tại A, đường cao AH
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Leftrightarrow \frac{1}{{A{H^2}}} = \frac{1}{{{6^2}}} + \frac{1}{{{8^2}}} = \frac{{25}}{{576}} \Rightarrow AH = \frac{{24}}{5} = 4,8cm\)
Đáp án B.
Câu 6: Cho \(\Delta ABC\) vuông tại \({\rm{A}}\), có \(AB = 3,AC = 4\). Khi đó tanB bằng
A. \(\frac{3}{4}\).
B. \(\frac{3}{5}\).
C. \(\frac{4}{3}\).
D. \(\frac{4}{5}\).
Phương pháp:
Áp dụng tỉ số lượng giác của góc nhọn
Lời giải:
Ta có \(\tan B = \frac{{AC}}{{AB}} = \frac{4}{3}\)
Đáp án C.
Phần II: Tự luận
Câu 7: (1,5d) Thực hiện phép tính:
a) \((3\sqrt 5 - 2\sqrt 3 ) \cdot \sqrt 5 + \sqrt {60} \).
b) \(\sqrt {125} - 4\sqrt {45} + 3\sqrt {20} + \sqrt {80} \).
Phương pháp:
Công thức khai phương căn bậc hai, trục căn thức.
Lời giải:
a) \((3\sqrt 5 - 2\sqrt 3 ) \cdot \sqrt 5 + \sqrt {60} = 3\sqrt {5.5} - 2\sqrt {3.5} + \sqrt {4.15} \) \( = 3.5 - 2\sqrt {15} + 2\sqrt {15} = 15\)
b) \(\sqrt {125} - 4\sqrt {45} + 3\sqrt {20} + \sqrt {80} = 5\sqrt 5 - 12\sqrt 5 + 6\sqrt 5 + 4\sqrt 5 = 3\sqrt 5 \)
Câu 8: (1,5đ) Giải phương trình:
a) \(\sqrt {4x + 20} + \sqrt {x + 5} - \frac{1}{3}\sqrt {9x + 45} = 4\);
b) \(\frac{{2\sqrt x - 7}}{3} + \sqrt x - \frac{{3\sqrt x - 5}}{2} = 1\)
Phương pháp:
a) Tìm điều kiện xác định, đưa các hệ số ra ngoài căn và rút gọn
b) Quy đồng bỏ mẫu và rút gọn, giải phương trình
Lời giải:
a) ĐKXĐ: \(x \ge - 5\)
Khi đó \(\sqrt {4x + 20} + \sqrt {x + 5} - \frac{1}{3}\sqrt {9x + 45} = 4\)
\( \Leftrightarrow \sqrt {4(x + 5)} + \sqrt {x + 5} - \frac{1}{3}\sqrt {9(x + 5)} = 4 \Leftrightarrow 2\sqrt {x + 5} + \sqrt {x + 5} - \frac{1}{3} \cdot 3\sqrt {x + 5} = 4\)
\( \Leftrightarrow 2\sqrt {x + 5} + \sqrt {x + 5} - \sqrt {x + 5} = 4 \Leftrightarrow \sqrt {x + 5} = 2 \Leftrightarrow x + 5 = 4\)
\( \Leftrightarrow x = - 1\) (thỏa mãn ĐKXĐ)
Vậy phương trình có nghiệm là \(x = - 1\)
b) ĐKXÐ: \(x \ge 0\)
Khi đó \(\frac{{2\sqrt x - 7}}{3} + \sqrt x - \frac{{3\sqrt x - 5}}{2} = 1 \Leftrightarrow 2(2\sqrt x - 7) + 6\sqrt x - 3(3\sqrt x - 5) = 6\)
\( \Leftrightarrow 4\sqrt x - 14 + 6\sqrt x - 9\sqrt x + 15 = 6 \Leftrightarrow \sqrt x = 5 \Leftrightarrow x = 25\) (thỏa mãn)
Vây phương trình có nghiệm là \(x = 25\)
Câu 9: (2đ) Cho biểu thức \(A = \frac{{{a^2} + \sqrt a }}{{a - \sqrt a + 1}} - \frac{{2a + \sqrt a }}{{\sqrt a }} + 1\) với \({\rm{a}} > 0\),
a) Rút gọn biểu thức \({\rm{A}}\).
b) Tìm \({\rm{a}}\) để \({\rm{A}} = 2\).
c) Tìm a để \({\rm{A}}\) đạt giá trị nhỏ nhất.
Phương pháp:
a) Rút gọn các phân thức rồi rút gọn biểu thức.
b) Giải phương trình \(A = 2\) tìm a
c) Áp dụng hằng đẳng thức.
Lời giải:
a) Với \(a > 0\) ta có:
\(\begin{array}{l}A = \frac{{{a^2} + \sqrt a }}{{a - \sqrt a + 1}} - \frac{{2a + \sqrt a }}{{\sqrt a }} + 1\\ = \frac{{\sqrt a \left( {\sqrt {{a^3}} + 1} \right)}}{{a - \sqrt a + 1}} - \frac{{\sqrt a (2\sqrt a + 1)}}{{\sqrt a }} + 1\\ = \frac{{\sqrt a (\sqrt a + 1)(a - \sqrt a + 1)}}{{a - \sqrt a + 1}} - (2\sqrt a + 1) + 1\\ = \sqrt a (\sqrt a + 1) - 2\sqrt a - 1 + 1\\ = a + \sqrt a - 2\sqrt a \\ = a - \sqrt a \end{array}\)
Vậy với \({\rm{a}} > 0\) thì \({\rm{A}} = a - \sqrt a \).
b) Để \({\rm{A}} = 2\) thì \(a - \sqrt a = 2 \Leftrightarrow a - \sqrt a - 2 = 0 \Leftrightarrow a + \sqrt a - 2\sqrt a - 2 = 0\)
\(\begin{array}{l} \Leftrightarrow \sqrt a (\sqrt a + 1) - 2(\sqrt a + 1) = 0\\ \Leftrightarrow (\sqrt a + 1)(\sqrt a - 2) = 0\\ \Leftrightarrow \sqrt a - 2 = 0({\rm{ do }}\sqrt a + 1 > 0)\\ \Leftrightarrow \sqrt a = 2 \Leftrightarrow a = 4(TM)\end{array}\)
Vậy \(a = 4\).
\(\begin{array}{l}{\rm{ c) A}} = a - \sqrt a \\ = a - 2\sqrt a \cdot \frac{1}{2} + \frac{1}{4} - \frac{1}{4}\\ = {\left( {\sqrt a - \frac{1}{2}} \right)^2} - \frac{1}{4} \ge - \frac{1}{4}\\ \Rightarrow {A_{\min }} = - \frac{1}{4} \Leftrightarrow \sqrt a - \frac{1}{2} = 0 \Leftrightarrow \sqrt a = \frac{1}{2} \Leftrightarrow a = \frac{1}{4}\end{array}\)
Vậy giá trị nhỏ nhất của \({\rm{A}}\) là \( - \frac{1}{4}\), đạt được khi \(a = \frac{1}{4}\).
Câu 10: (2đ) Cho \(\Delta ABC\) vuông tại A có \(\widehat B = {30^0},AB = 6\;{\rm{cm}}\).
a) Giải \(\Delta ABC\).
b) Vẽ đường cao \({\rm{AH}}\) và trung tuyến \({\rm{AM}}\) của \(\Delta ABC\). Tính diện tích \(\Delta AHM\).
Phương pháp:
Áp dụng tỉ số lượng giác góc nhọn \(\sin ,\cos ,\tan ,\cot \).
Lời giải:
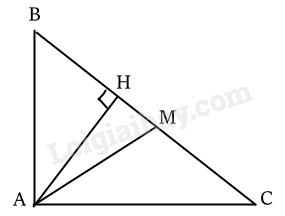
a) Ta có \(\widehat C = {90^0} - \widehat B = {90^0} - {30^0} = {60^0}\)
Xét \(\Delta ABC\) vuông tại \({\rm{A}}\), đường cao \({\rm{AH}}\). Ta có :
\(\begin{array}{l}AC = AB.\tan B = 6.\tan {30^0} = 2\sqrt 3 \;{\rm{cm}}\\BC = \frac{{AB}}{{\cos {\rm{B}}}} = \frac{6}{{\cos {{30}^0}}} = 4\sqrt 3 \;{\rm{cm}}\end{array}\)
b) Xét \(\Delta ABH, \) ta có \(AH = AB.\sin B = 6.\sin {30^0} = 6 \cdot \frac{1}{2} = 3\;{\rm{cm}}\\HB = AB.\cos B = 6.\cos {30^0} = 6 \cdot \frac{{\sqrt 3 }}{2} = 3\sqrt 3 \;{\rm{cm}}\\MB = \frac{{BC}}{2} = \frac{{4\sqrt 3 }}{2} = 2\sqrt 3 \;{\rm{cm}}\\HM = HB - MB = 3\sqrt 3 - 2\sqrt 3 = \sqrt 3 \;{\rm{cm}}\)
Diện tích \(\Delta AHM\) là: \({S_{\Delta AHM}} = \frac{{AH \cdot HM}}{2} = \frac{{3 \cdot \sqrt 3 }}{2} \approx 2,6\;{\rm{c}}{{\rm{m}}^2}\)
- Đề kiểm tra giữa kì 1 Toán 9 - Đề số 14 có lời giải chi tiết
- Đề kiểm tra giữa kì 1 Toán 9 - Đề số 15 có lời giải chi tiết
- Tổng hợp 15 đề kiểm tra giữa học kì 1 Toán 9 có đáp án
- Đề kiểm tra giữa kì 1 Toán 9 - Đề số 12 có lời giải chi tiết
- Đề kiểm tra giữa kì 1 Toán 9 - Đề số 11 có lời giải chi tiết
>> Xem thêm













Danh sách bình luận