 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Đề ôn tập học kì 1 – Có đáp án và lời giải
Đề ôn tập học kì 1 – Có đáp án và lời giải
Đề số 17 - Đề kiểm tra học kì 1 - Toán 9
Tải vềĐáp án và lời giải chi tiết Đề số 17 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9
Đề bài
I. TRẮC NGHIỆM (1 điểm)Trả lời câu hỏi bằng cách viết lại chữ cái trước đáp án đúng vào bài làm:
Câu 1 : Nếu x thỏa mãn điều kiện \(\sqrt {3 + \sqrt x } = 2\) thì x nhận giá trị là:
A. 0 B. 4
C. 5 D. 1
Câu 2 : Điều kiện để hàm số bậc nhất \(y = \left( {1 - m} \right)x + m\,\,\left( {m \ne 1} \right)\)là hàm số nghịch biến là:
A. \(m > 1\) B. \(m \ge 1\)
C. \(m \le 1\) D. \(m < 1\)
Câu 3 : Cho tam giác MNP vuông tại M, đường cao MH. Chọn hệ thức sai:
A. \(M{H^2} = HN.HP\)
B. \(M{P^2} = NH.HP\)
C. \(MH.NP = MN.MP\)
D. \(\dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}} = \dfrac{1}{{M{H^2}}}\)
Câu 4 : Cho hai đường tròn \(\left( {I;7cm} \right)\)và \(\left( {K;5cm} \right)\). Biết \(IK = 2cm\). Quan hệ giữa hai đường tròn là:
A. Tiếp xúc trong
B. Tiếp xúc ngoài
C. Cắt nhau
D. Đựng nhau
II. TỰ LUẬN (9 điểm)
Câu 1 (1 điểm):Thực hiện phép tính: a) \(3\sqrt {\dfrac{1}{3}} + 4\sqrt {12} - 5\sqrt {27} \) b) \(\dfrac{{3 + 2\sqrt 3 }}{{\sqrt 3 }} - \dfrac{2}{{\sqrt 3 - 1}}\)
Câu 2 (2 điểm): Cho biểu thức \(P = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{x - 2\sqrt x }}{{x - 4}}\) và \(Q = \dfrac{{\sqrt x + 2}}{{\sqrt x - 2}}\,\,\left( {x \ge 0;x \ne 4} \right)\)
a) Rút gọn P
b) Tìm x sao cho \(P = 2\)
c) Biết \(M = P:Q\). Tìm giá trị của x để \({M^2} < \dfrac{1}{4}\)
Câu 3 (2 điểm):Cho hàm số \(y = \left( {m - 4} \right)x + 4\) có đồ thị là đường thẳng \(\left( d \right)\)\(\left( {m \ne 4} \right)\).
a) Tìm m để đồ thị hàm số đi qua \(A\left( {1;6} \right)\)
b) Vẽ đồ thị hàm số với m tìm được ở câu a. Tính góc tạo bởi đồ thị hàm số vừa vẽ với trục Ox (làm tròn đến phút).
c) Tìm m để đường thẳng \(\left( d \right)\) song song với đường thẳng\(\left( {{d_1}} \right):y = \left( {m - {m^2}} \right)x + m + 2\)
Câu 4 (3,5 điểm):Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn \(\left( O \right)\) (với E là tiếp điểm). Vẽ dây EH vuông góc với AO tại M.
a) Cho biết bán kính \(R = 5cm,\,\,OM = 3cm\). Tính độ dài dây EH.
b) Chứng minh AH là tiếp tuyến của đường tròn\(\left( O \right)\).
c) Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn \(\left( O \right)\) (F là tiếp điểm). Chứng minh 3 điểm E, O, F thẳng hàng và \(BF.AE = {R^2}\).
d) Trên tia HB lấy điểm I (\(I \ne B\)), qua I vẽ tiếp tuyến thứ hai với đường tròn \(\left( O \right)\) cắt các đường thẳng BF, AE lần lượt tại C và D. Vẽ đường thẳng IF cắtAE tại Q. Chứng minh \(AE = DQ\).
Câu 5 (0,5 điểm):Cho x,y là các số thực dương thỏa mãn \(x + y \le 1\).
Tìm giá trị nhỏ nhất của biểu thức \(P = \left( {\dfrac{1}{x} + \dfrac{1}{y}} \right).\sqrt {1 + {x^2}{y^2}} \).
LG trắc nghiệm
Lời giải chi tiết:
I. TRẮC NGHIỆM
|
1D |
2A |
3B |
4A |
LG bài 1
Lời giải chi tiết:
a) \(3\sqrt {\dfrac{1}{3}} + 4\sqrt {12} - 5\sqrt {27} = \sqrt 3 + 8\sqrt 3 - 15\sqrt 3 = - 6\sqrt 3 \)
b) \(\dfrac{{3 + 2\sqrt 3 }}{{\sqrt 3 }} - \dfrac{2}{{\sqrt 3 - 1}} = \dfrac{{\left( {\sqrt 3 + 2} \right)\sqrt 3 }}{{\sqrt 3 }} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} = \sqrt 3 + 2 - \sqrt 3 - 1 = 1\)
LG bài 2
Lời giải chi tiết:
Cho biểu thức \(P = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{x - 2\sqrt x }}{{x - 4}}\) và \(Q = \dfrac{{\sqrt x + 2}}{{\sqrt x - 2}}\,\,\left( {x \ge 0;x \ne 4} \right)\)
a) Rút gọn P
\(\begin{array}{l}P = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{x - 2\sqrt x }}{{x - 4}}\\\;\;\; = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{\sqrt x \left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\\;\; = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{\sqrt x }}{{\sqrt x + 2}} = \dfrac{{\sqrt x }}{{\sqrt x - 2}}\end{array}\)
b) Tìm x sao cho \(P = 2\)
\(P = 2 \Leftrightarrow \dfrac{{\sqrt x }}{{\sqrt x - 2}} = 2 \)
\(\Leftrightarrow \sqrt x = 2\sqrt x - 4 \)
\(\Leftrightarrow \sqrt x = 4 \Leftrightarrow x = 16\)
c) Biết \(M = P:Q\). Tìm giá trị của x để \({M^2} < \dfrac{1}{4}\)
\(M = P:Q = \dfrac{{\sqrt x }}{{\sqrt x - 2}}.\dfrac{{\sqrt x - 2}}{{\sqrt x + 2}} = \dfrac{{\sqrt x }}{{\sqrt x + 2}}\)
\({M^2} < \dfrac{1}{4} \Leftrightarrow {\left( {\dfrac{{\sqrt x }}{{\sqrt x + 2}}} \right)^2} < \dfrac{1}{4} \)
\(\Leftrightarrow \dfrac{{\sqrt x }}{{\sqrt x + 2}} < \dfrac{1}{2}\)
\(\Leftrightarrow 2\sqrt x < \sqrt x + 2 \Leftrightarrow \sqrt x < 2 \Leftrightarrow x < 4\)
Kết hợp điều kiện đầu bài \( \Rightarrow 0 \le x < 4\)
LG bài 3
Lời giải chi tiết:
Cho hàm số \(y = \left( {m - 4} \right)x + 4\) có đồ thị là đường thẳng \(\left( d \right)\)\(\left( {m \ne 4} \right)\).
a) Tìm m để đồ thị hàm số đi qua \(A\left( {1;6} \right)\)
\(A\left( {1;\;6} \right)\) thuộc đường thẳng \(\left( d \right).\) Ta thay \(x = 1;\,\,y = 6\) vào hàm số \(y = \left( {m - 4} \right)x + 4\) ta được \(6 = \left( {m - 4} \right).1 + 4 \Leftrightarrow m = 6\;\;\left( {tm} \right)\)
Vậy với\(m = 6\) thì đồ thị hàm số đi qua \(A\left( {1;6} \right)\)
b) Vẽ đồ thị hàm số với m tìm được ở câu a. Tính góc tạo bởi đồ thị hàm số vừa vẽ với trục Ox (làm tròn đến phút).
Với \(m = 6\) thì \(y = 2x + 4\)
Ta có bảng giá trị:
|
x |
0 |
-2 |
|
\(y = 2x + 4\) |
4 |
0 |
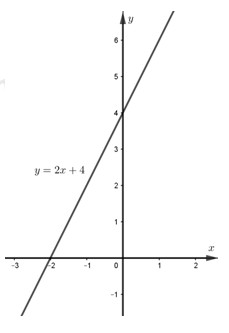
Đường thẳng \(y = 2x + 4\) đi qua hai điểm \(\left( {0;4} \right)\) và \(\left( { - 2;0} \right)\)
Gọi \(\alpha \) là góc tạo bởi đồ thị hàm số vừa vẽ với trụcOx \( \Rightarrow \tan \alpha = 2 \Rightarrow \alpha \approx {63^o}{26'}\)
c) Tìm m để đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {{d_1}} \right):y = \left( {m - {m^2}} \right)x + m + 2\)
\(\left( d \right)//\left( {{d_1}} \right) \Leftrightarrow \left\{ \begin{array}{l}m - {m^2} = m - 4\\m + 2 \ne 4\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{m^2} = 4\\m \ne 2\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\\m \ne 2\end{array} \right. \Leftrightarrow m = - 2\;\;\left( {tm} \right)\)
Vậy với \(m = - 2\) thỏa mãn yêu cầu đề bài.
LG bài 4
Lời giải chi tiết:
Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn \(\left( O \right)\) (với E là tiếp điểm). Vẽ dây EH vuông góc với AO tại M.
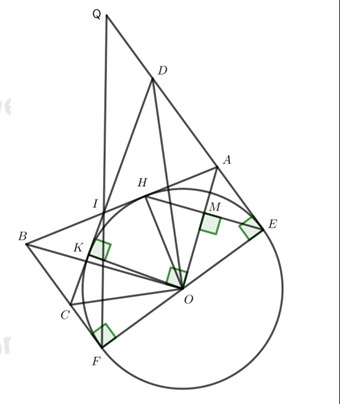
a) Cho biết bán kính \(R = 5cm,\,\,OM = 3cm\). Tính độ dài dây EH.
Theo đề bài ta có: \(EH \bot OA\) tại M nên M là trung điểm của EH hay \(EH = 2EM\)(định lý mối liên hệ giwuax đường kính và dây cung)
Áp dụng định lý Pi-ta-go cho tam giác vuông OME có:
\(EM = \sqrt {O{E^2} - O{M^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Vậy \(EH = 2EM = 8\,\,(cm)\)
b) Chứng minh AH là tiếp tuyến của đường tròn \(\left( O \right)\).
Ta có \(\left\{ \begin{array}{l}OA \bot EH\\ME = MH\end{array} \right. \Rightarrow \)OA là đường trung trực của EH\( \Rightarrow AE = AH\)
Xét hai tam giác OEA và tam giác OHA có:
\(OE = OH\,\,( = R);\,\,\,AE = AH;\,\,OA\)chung
\( \Rightarrow \Delta OEA = \Delta OHA\)(c.c.c) \( \Rightarrow \angle OHA = \angle OEA = {90^o}\) hay \(AH \bot OH\)
Vậy AH là tiếp tuyến của \(\left( O \right)\) (đpcm).
c) Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn \(\left( O \right)\) (F là tiếp điểm). Chứng minh 3 điểm E, O, F thẳng hàng và \(BF.AE = {R^2}\).
Có \(AH \bot OH\;\;\left( {cmt} \right)\) hay Blà giao của hai tiếp tuyến BH; BF
\( \Rightarrow \angle BOF = \angle BOH\), lại có \(\angle EOA = \angle HOA\)
\( \Rightarrow \angle EOA + \angle AOB + \angle BOF = 2\left( {\angle AOH + \angle BOH} \right) = 2\angle AOB = {180^o}\)
\( \Rightarrow \)E, O, F thẳng hàng. (đpcm)
Có \(\angle EOA + \angle BOF = {180^o} - \angle AOB = {90^o} \Rightarrow \angle OAE = \angle BOF\) (cùng phụ \(\angle AOE\))
Xét \(\Delta AOE\) và \(\Delta OBF\)có: \(\angle OAE = \angle BOF\); \(\angle AEO = \angle BFO = {90^o}\)
\( \Rightarrow \dfrac{{AE}}{{OF}} = \dfrac{{OE}}{{BF}} \Rightarrow AE.BF = OE.OF = {R^2}\,\,\,\,\,\left( 1 \right)\)
d) Trên tia HB lấy điểm I (\(I \ne B\)), qua I vẽ tiếp tuyến thứ hai với đường tròn \(\left( O \right)\) cắt các đường thẳng BF, AE lần lượt tại C và D. Vẽ đường thẳng IF cắt AE tại Q. Chứng minh \(AE = DQ\).
Có \(BF//AQ\) (do cùng vuông góc với EF) \( \Rightarrow \dfrac{{BF}}{{CF}} = \dfrac{{AQ}}{{DQ}}\)(định lý Talet) (*)
Dễ dàng chứng minh \(\Delta COD\) vuông tại O. Gọi K là tiếp điểm của tiếp tuyến thứ 2 qua I với \(\left( O \right)\)
Áp dụng hệ thức lượng trong tam giác vuông COD đường cao DK ta có: \(O{K^2} = DK.CK\)
Mà DE, DK là các tiếp tuyến của \(\left( O \right)\)cắt nhau tại D nên \(DE = DK\)
Tương tự \(CK = CF \Rightarrow O{K^2} = CF.DE \Leftrightarrow CF.DE = {R^2}\,\,\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\)và \(\left( 2 \right)\) suy ra: \(CF.DE = AE.BF \Leftrightarrow \dfrac{{BF}}{{CF}} = \dfrac{{DE}}{{AE}}\) (**)
Từ (*) và (**) suy ra: \(\dfrac{{AQ}}{{DQ}} = \dfrac{{DE}}{{AE}} \Leftrightarrow \dfrac{{AQ}}{{AQ - DQ}} = \dfrac{{DE}}{{DE - AE}} \Leftrightarrow \dfrac{{AQ}}{{AD}} = \dfrac{{DE}}{{AD}} \Leftrightarrow AQ = DE\)
Câu 5:
Cho x,y là các số thực dương thỏa mãn \(x + y \le 1\).
Tìm giá trị nhỏ nhất của biểu thức \(P = \left( {\dfrac{1}{x} + \dfrac{1}{y}} \right).\sqrt {1 + {x^2}{y^2}} \).
Có x, y là các số thực dương \( \Rightarrow \dfrac{1}{x};\dfrac{1}{y}\) là các số thực dương
Áp dụng bất đẳng thức Cô-si ta được : \(\dfrac{1}{x} + \dfrac{1}{y} \ge 2\sqrt {\dfrac{1}{x}.\dfrac{1}{y}} = \dfrac{2}{{\sqrt {xy} }}\)
Vậy \(P \ge \dfrac{2}{{\sqrt {xy} }}.\sqrt {1 + {x^2}{y^2}} = 2\sqrt {\dfrac{1}{{xy}} + xy} \)
Ta có : \(1 \ge x + y \ge 2\sqrt {xy} \)(do x, y là hai số thực dương)\( \Rightarrow xy \le \dfrac{1}{4}\)
\(\dfrac{1}{{xy}} + xy = \dfrac{1}{{16xy}} + xy + \dfrac{{15}}{{16}}.\dfrac{1}{{xy}} \ge 2\sqrt {\dfrac{1}{{16xy}}.xy} + \dfrac{{15}}{{16}}\dfrac{1}{{\dfrac{1}{4}}} = 2.\dfrac{1}{4} + \dfrac{{15}}{4} = \dfrac{{17}}{4}\)
\( \Rightarrow P \ge 2\sqrt {\dfrac{{17}}{4}} = \sqrt {17} \). Dấu ‘=’ xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x = y\\x + y = 1\\xy = \dfrac{1}{4}\end{array} \right. \Leftrightarrow x = y = \dfrac{1}{2}\)
Vậy giá trị nhỏ nhất của P là \(\sqrt {17} \) đạt được khi \(x = y = \dfrac{1}{2}.\)
Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 9 tại Tuyensinh247.com
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận