 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Đề thi học kì 2 của các trường có lời giải – Mới nhất
Đề thi học kì 2 của các trường có lời giải – Mới nhất
Đề thi học kì 2 môn toán lớp 9 năm 2019 - 2020 Sở GD tỉnh Vĩnh Phúc
Giải chi tiết đề thi học kì 2 môn toán lớp 9 năm 2019 - 2020 Sở GD tỉnh Vĩnh Phúc với cách giải nhanh và chú ý quan trọng
Đề bài
PHẦN I: TRẮC NGHIỆM (3 điểm).
Câu 1. Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = - 2\\2x + y = - 1\end{array} \right.\) là
A. \(\left( {x;y} \right) = \left( {1; - 1} \right)\)
B. \(\left( {x;y} \right) = \left( { - 1;1} \right)\)
C. \(\left( {x;y} \right) = \left( { - 2;0} \right)\)
D. \(\left( {x;y} \right) = \left( {0; - 1} \right)\)
Câu 2. Phương trình bậc hai \( - 2{x^2} + 4x - 1 = 0\) có tổng hai nghiệm bằng
A. \(2\) B. \( - 2\)
C. \(1\) D. \( - 1\)
Câu 3. Phương trình bậc hai \({x^2} + x - 1 = 0\) có biệt thức \(\Delta \) bằng
A. \(3\) B. \( - 3\)
C. \(2\) D. \(5\)
Câu 4. Cho đường tròn \(\left( {O;4\,cm} \right)\). Khi đó độ dài đường tròn bằng
A. \(4\pi \,cm\) B. \(16\pi \,c{m^2}\)
C. \(8\pi \,cm\) D. \(8\pi \,c{m^2}\)
Câu 5. Một hình quạt tròn có bán kính \(4\,cm\), số đo cung là \({36^0}\). Khi đó diện tích hình quạt tròn bằng
A. \(1,6\pi \,c{m^2}\) B. \(0,4\pi \,c{m^2}\)
C. \(0,8\pi \,c{m^2}\) D. \(1,2\pi \,c{m^2}\)
Câu 6. Độ dài cung \({60^0}\) của một đường tròn có bán kính \(6\,cm\) là
A. \(9\pi \,cm\) B. \(2\pi \,cm\)
C. \(6\pi \,cm\) D. \(3\pi \,cm\)
PHẦN II: TỰ LUẬN (7 điểm).
Câu 7: (1,5 điểm)
a) Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 3\\x + y = 0\end{array} \right.\)
b) Giải phương trình \({x^4} + {x^2} - 6 = 0\).
Câu 8: (1,0 điểm)
Cho phương trình \({x^2} - 2mx + m - 2 = 0\,\,\left( 1 \right)\) (\(x\) là ẩn, \(m\) là tham số)
a) Giải phương trình (1) khi \(m = 1\).
b) Chứng minh rằng phương trình (1) có nghiệm với mọi \(m\).
Câu 9: (1,5 điểm)
Theo kế hoạch trong tháng 3 năm 2020, hai tổ công nhân dự kiến may \(7000\) chiếc khẩu trang để phục vụ cho công tác phòng chống dịch Covid-19. Nhưng thực tế tổ I đã may vượt mức kế hoạch 10%, tổ II may vượt mức kế hoạch 12% nên cả hai tổ đã may được \(7780\) chiếc khẩu trang. Hỏi theo kế hoạch mỗi tổ phải may bao nhiêu chiếc khẩu trang?
Câu 10: (2,5 điểm)
Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) kẻ hai tiếp tuyến \(MA,MB\) với đường tròn \(\left( O \right)\) (\(A,B\) là các tiếp điểm). Lấy điểm \(N\) bất kì trên cung nhỏ \(AB\) (\(N\) không trùng với \(A,B\)). Gọi \(H,I,K\) lần lượt là chân đường vuông góc kẻ từ \(N\) đến các đường thẳng \(AM,AB,MB\).
a) Chứng minh \(AHNI\) là tứ giác nội tiếp.
b) Chứng minh \(\widehat {NIH} = \widehat {NBA}\).
c) Gọi giao điểm của \(HI\) và \(AN\) là \(P\), \(KI\) và \(NB\) là \(Q\). Chứng minh \(PQ\) song song với \(AB\).
Câu 11: (0,5 điểm)
Cho \(a,b,c\) là các số thực dương thỏa mãn \(a + b + c = 3\). Chứng minh rằng \(\dfrac{{{a^2}\left( {b + 1} \right)}}{{a + b + ab}} + \dfrac{{{b^2}\left( {c + 1} \right)}}{{b + c + bc}} + \dfrac{{{c^2}\left( {a + 1} \right)}}{{c + a + ca}} \ge 2\)
Đ/a TN
|
1B |
2A |
3D |
4C |
5A |
6B |
Câu 1 (TH):
Phương pháp:
Giải hệ phương trình bằng phương pháp cộng đại số
Cách giải:
Ta có: \(\left\{ \begin{array}{l}x - y = - 2\\2x + y = - 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3x = - 3\\x - y = - 2\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\ - 1 - y = - 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\end{array}\)
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( { - 1;1} \right)\)
Chọn B
Câu 2 (TH):
Phương pháp:
Dùng hệ thức Vi-et cho phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm \({x_1};{x_2}\) thì \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)
Cách giải:
Ta có: \(\Delta ' = {2^2} - \left( { - 2} \right).\left( { - 1} \right) = 2 > 0\) nên phương trình đã cho có hai nghiệm \({x_1};{x_2}.\)
Theo hệ thức Vi-ét ta có: \({x_1} + {x_2} = - \dfrac{b}{a}\) \( = - \dfrac{4}{{ - 2}} = 2\)
Chọn A
Câu 3 (NB):
Phương pháp:
Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có \(\Delta = {b^2} - 4ac\)
Cách giải:
Ta có: \(\Delta = {b^2} - 4ac\) \( = {1^2} - 4.1.\left( { - 1} \right) = 5\)
Chọn D
Câu 4 (TH):
Phương pháp:
Độ dài đường tròn bán kính \(R\) là \(C = 2\pi R\)
Cách giải:
Độ dài đường tròn \(C = 2\pi R\) \( = 2\pi .4 = 8\pi \) (cm)
Chọn C
Câu 5 (TH):
Phương pháp:
Diện tích quạt tròn có bán kính \(r\) và số đo cung là \({n^0}\) là \(S = \dfrac{{\pi {r^2}n}}{{360}}\)
Cách giải:
Diện tích quạt tròn là \({S_q} = \dfrac{{\pi {r^2}n}}{{360}}\) \( = \dfrac{{\pi {4^2}.36}}{{360}} = 1,6\pi \left( {c{m^2}} \right)\)
Chọn A
Câu 6 (TH):
Phương pháp:
Độ dài cung tròn có bán kính \(r\) và số đo cung là \({n^0}\) là \(l = \dfrac{{\pi rn}}{{180}}\)
Cách giải:
Độ dài cung là \(l = \dfrac{{\pi .6.60}}{{180}} = 2\pi \left( {cm} \right)\)
Chọn B
LG câu 7
Phương pháp giải:
a) Giải hệ phương trình bằng phương pháp cộng đại số
b) Đặt \({x^2} = t\left( {t \ge 0} \right)\) sau đó đưa về giải phương trình bậc hai ẩn \(t\)
So sánh điều kiện rồi thay lại cách đặt để tìm \(x.\)
Lời giải chi tiết:
a) Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 3\\x + y = 0\end{array} \right.\)
Ta có:
\(\left\{ \begin{array}{l}2x - y = 3\\x + y = 0\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}3x = 3\\x + y = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\1 + y = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 1\end{array} \right.\end{array}\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {1; - 1} \right)\)
b) Giải phương trình \({x^4} + {x^2} - 6 = 0\).
Đặt \({x^2} = t\left( {t \ge 0} \right)\), ta được phương trình \({t^2} + t - 6 = 0\)
\(\begin{array}{l} \Leftrightarrow {t^2} + 3t - 2t - 6 = 0\\ \Leftrightarrow t\left( {t + 3} \right) - 2\left( {t + 3} \right) = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {t + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = 2\left( {tm} \right)\\t = - 3\left( {ktm} \right)\end{array} \right.\end{array}\)
Với \(t = 2 \Rightarrow {x^2} = 2\) \( \Leftrightarrow x = \pm \sqrt 2 \)
Vậy phương trình đã cho có tập nghiệm \(S = \left\{ { - \sqrt 2 ;\sqrt 2 } \right\}\)
LG câu 8
Phương pháp giải:
a) Thay \(m = 1\) vào phương trình rồi giải
b) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có nghiệm \( \Leftrightarrow \Delta ' \ge 0\)
Lời giải chi tiết:
Cho phương trình \({x^2} - 2mx + m - 2 = 0\,\,\left( 1 \right)\) (\(x\) là ẩn, \(m\) là tham số)
a) Giải phương trình (1) khi \(m = 1\).
Thay \(m = 1\) vào phương trình \(\left( 1 \right)\) ta được: \({x^2} - 2x - 1 = 0\) (*)
Có \(\Delta ' = {1^2} - 1.\left( { - 1} \right) = 2\) nên phương trình (*) có hai nghiệm phân biệt \(\left[ \begin{array}{l}x = 1 + \sqrt 2 \\x = 1 - \sqrt 2 \end{array} \right.\)
Vậy với \(m = 1\) phương trình đã cho có hai nghiệm phân biệt \(x = 1 + \sqrt 2 ;x = 1 - \sqrt 2 \)
b) Chứng minh rằng phương trình (1) có nghiệm với mọi \(m\).
Ta thấy phương trình \(\left( 1 \right)\) có \(a = 1 \ne 0\) nên nó là phương trình bậc hai một ẩn
Lại có \(\Delta ' = {\left( { - m} \right)^2} - 1.\left( {m - 2} \right)\) \( = {m^2} - m + 2\) \( = {m^2} - 2m.\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{7}{4}\) \( = {\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{7}{4}\)
Vì \({\left( {m - \dfrac{1}{2}} \right)^2} \ge 0\) với mọi \(m\) nên \({\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{7}{4} \ge \dfrac{7}{4} > 0\) với mọi \(m.\)
Suy ra \(\Delta ' > 0\) với mọi \(m\) nên phương trình (1) luôn có hai nghiệm phân biệt với mọi \(m.\)
LG câu 9
Phương pháp giải:
Giải bài toán bằng cách lập hệ phương trình
B1: Chọn ẩn và đặt điều kiện cho ẩn
B2: Lập và giải hệ phương trình
B3: So sánh điều kiện và kết luận nghiệm
Lời giải chi tiết:
Gọi số khẩu trang mà tổ 1 và tổ 2 phải may theo kế hoạch lần lượt là \(x;y\) (chiếc) \(\left( {0 < x,y < 7000} \right)\)
Vì hai tổ dự kiến may 7000 chiếc khẩu trang nên ta có phương tình \(x + y = 7000\) (1)
Thực tế tổ 1 may vượt kế hoạch 10% nên tổ 1 may được \(\left( {1 + 10\% } \right)x = 1,1x\) chiếc
Thực tế tổ 2 may vượt kế hoạch 12% nên tổ 2 may được \(\left( {1 + 12\% } \right)y = 1,12y\) chiếc
Thực tế cả hai tổ may được \(7780\) chiếc nên ta có phương trình \(1,1x + 1,12y = 7780\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y = 7000\\1,1x + 1,12y = 7780\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}1,1x + 1,1y = 7700\\1,1x + 1,12y = 7780\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0,02y = 80\\x + y = 7000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 4000\\x + 4000 = 7000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 4000\left( {tm} \right)\\x = 3000\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy theo kế hoạch, tổ 1 phải may 3000 chiếc khẩu trang và tổ 2 phải may 4000 chiếc khẩu trang.
LG câu 10
Phương pháp giải:
a) Chứng minh tứ giác có tổng hai góc đối bằng \({180^0}\).
b) Sử dụng tính chất của tứ giác nội tiếp suy tra \(\widehat {NIH} = \widehat {NAH}\).
Từ đó suy điều phải chứng minh.
c) Chứng minh \(\widehat {ANI} = \widehat {BNK} = \widehat {KIB},\) \(\widehat {BNI} = \widehat {ANH} = \widehat {AIH}\)
Từ đó suy ra \(\widehat {ANB} + \widehat {HIK} = {180^0}\) và tứ giác \(PNQI\) nội tiếp.
Sử dụng tính chất tứ giác \(PNQI\) nội tiếp để chứng minh \(PQ//AB\).
Lời giải chi tiết:
Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) kẻ hai tiếp tuyến \(MA,MB\) với đường tròn \(\left( O \right)\) (\(A,B\) là các tiếp điểm). Lấy điểm \(N\) bất kì trên cung nhỏ \(AB\) (\(N\) không trùng với \(A,B\)). Gọi \(H,I,K\) lần lượt là chân đường vuông góc kẻ từ \(N\) đến các đường thẳng \(AM,AB,MB\).
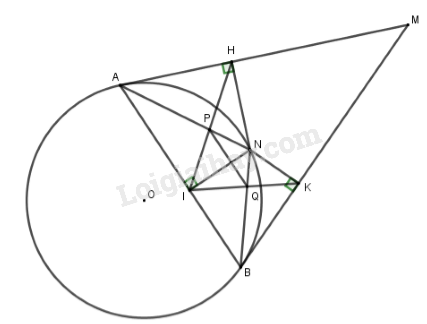
a) Chứng minh \(AHNI\) là tứ giác nội tiếp.
Ta có: \(NH \bot AM \Rightarrow \widehat {NHA} = {90^0}\)
\(NI \bot AB \Rightarrow \widehat {NIA} = {90^0}\)
Tứ giác \(AHNI\) có: \(\widehat {NHA} + \widehat {NIA} = {90^0} + {90^0} = {180^0}\).
Vậy \(AHNI\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)) (đpcm).
b) Chứng minh \(\widehat {NIH} = \widehat {NBA}\).
Theo câu a, \(AHNI\) là tứ giác nội tiếp
\( \Rightarrow \) \(\widehat {NIH} = \widehat {NAH}\) (góc nội tiếp cùng chắn cung \(NH\)) (1)
Lại có, \(\widehat {NAH} = \widehat {NBA}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(AN\)) (2)
Từ (1) và (2) suy ra \(\widehat {NIH} = \widehat {NBA}\) \(\left( { = \widehat {NAH}} \right)\) (đpcm).
c) Gọi giao điểm của \(HI\) và \(AN\) là \(P\), \(KI\) và \(NB\) là \(Q\). Chứng minh \(PQ\) song song với \(AB\).
Ta có:
\(\widehat {HNA} + \widehat {HAN} = {90^0}\)
\(\widehat {BNI} + \widehat {NBA} = {90^0}\)
Mà \(\widehat {HAN} = \widehat {NBA}\) (chắn cung \(AN\))
\( \Rightarrow \widehat {HNA} = \widehat {BNI}\)
Mà \(\widehat {HNA} = \widehat {HIA}\)(cùng chắn cung \(HA\))
Nên \(\widehat {BNI} = \widehat {HIA}\) (3)
Tương tự,
\(\begin{array}{l}\widehat {KNB} + \widehat {KBN} = {90^0}\\\widehat {ANI} + \widehat {NAB} = {90^0}\end{array}\)
Mà \(\widehat {KBN} = \widehat {NAB}\) (cùng chắn cung \(BN\))
\( \Rightarrow \widehat {KNB} = \widehat {ANI}\)
Lại có tứ giác \(BKNI\) nội tiếp (vì \(\widehat {BKI} + \widehat {BIN} = {90^0} + {90^0} = {180^0}\)) nên:
\(\widehat {KNB} = \widehat {KIB}\) (cùng chắn cung \(BK\))
\( \Rightarrow \widehat {ANI} = \widehat {KIB}\) (4)
Từ (3) và (4) suy ra
\(\begin{array}{l}\widehat {BNI} + \widehat {ANI} = \widehat {HIA} + \widehat {KIB}\\ \Rightarrow \widehat {BNA} = \widehat {HIA} + \widehat {KIB}\\ \Rightarrow \widehat {BNA} + \widehat {PIQ} = \widehat {HIA} + \widehat {KIB} + \widehat {PIQ}\\ \Rightarrow \widehat {BNA} + \widehat {PIQ} = {180^0}\end{array}\)
\( \Rightarrow \widehat {PNQ} + \widehat {PIQ} = {180^0}\)
\( \Rightarrow \) tứ giác \(PNIQ\) nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\))
\( \Rightarrow \widehat {NQP} = \widehat {NIP} = \widehat {NIH}\)
Mà \(\widehat {NIH} = \widehat {NBA}\left( {cmt} \right)\)
\( \Rightarrow \widehat {NQP} = \widehat {NBA}\left( { = \widehat {NIP}} \right)\)
Mà hai góc này ở vị trí đồng vị nên \(PQ//AB\) (đpcm).
LG câu 11
Phương pháp giải:
Chứng minh và sử dụng bất đẳng thức \(\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} + \dfrac{{{z^2}}}{c} \ge \dfrac{{{{\left( {x + y + z} \right)}^2}}}{{a + b + c}}\)
Lời giải chi tiết:
Cho \(a,b,c\) là các số thực dương thỏa mãn \(a + b + c = 3\). Chứng minh rằng \(\dfrac{{{a^2}\left( {b + 1} \right)}}{{a + b + ab}} + \dfrac{{{b^2}\left( {c + 1} \right)}}{{b + c + bc}} + \dfrac{{{c^2}\left( {a + 1} \right)}}{{c + a + ca}} \ge 2\)
Trước hết ta chứng minh BĐT \(\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} + \dfrac{{{z^2}}}{c} \ge \dfrac{{{{\left( {x + y + z} \right)}^2}}}{{a + b + c}}\) (*)
Áp dụng BĐT Bunhia cho các bộ số \(\left( {\dfrac{x}{{\sqrt a }},\dfrac{y}{{\sqrt b }},\dfrac{z}{{\sqrt c }}} \right)\) và \(\left( {\sqrt a ;\sqrt b ;\sqrt c } \right)\) ta có:
\(\begin{array}{l}\left( {\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} + \dfrac{{{z^2}}}{c}} \right)\left( {a + b + c} \right)\\ \ge {\left( {\dfrac{x}{{\sqrt a }}.\sqrt a + \dfrac{y}{{\sqrt b }}.\sqrt b + \dfrac{z}{{\sqrt c }}.\sqrt c } \right)^2}\\ = {\left( {x + y + z} \right)^2}\\ \Rightarrow \left( {\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} + \dfrac{{{z^2}}}{c}} \right)\left( {a + b + c} \right) \ge {\left( {x + y + z} \right)^2}\\ \Rightarrow \dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} + \dfrac{{{z^2}}}{c} \ge \dfrac{{{{\left( {x + y + z} \right)}^2}}}{{a + b + c}}\end{array}\)
Vậy (*) được chứng minh.
Ta có:
\(\begin{array}{l}P = \dfrac{{{a^2}\left( {b + 1} \right)}}{{a + b + ab}} + \dfrac{{{b^2}\left( {c + 1} \right)}}{{b + c + bc}} + \dfrac{{{c^2}\left( {a + 1} \right)}}{{c + a + ca}}\\ = \dfrac{{{a^2}\left( {b + 1} \right)}}{{b + a\left( {b + 1} \right)}} + \dfrac{{{b^2}\left( {c + 1} \right)}}{{c + b\left( {c + 1} \right)}} + \dfrac{{{c^2}\left( {a + 1} \right)}}{{a + c\left( {a + 1} \right)}}\\ = \dfrac{{{a^2}}}{{\dfrac{b}{{b + 1}} + a}} + \dfrac{{{b^2}}}{{\dfrac{c}{{c + 1}} + b}} + \dfrac{{{c^2}}}{{\dfrac{a}{{a + 1}} + c}}\\ \ge \dfrac{{{{\left( {a + b + c} \right)}^2}}}{{\dfrac{b}{{b + 1}} + a + \dfrac{c}{{c + 1}} + b + \dfrac{a}{{a + 1}} + c}}\\ = \dfrac{9}{{3 + \dfrac{b}{{b + 1}} + \dfrac{c}{{c + 1}} + \dfrac{a}{{a + 1}}}}\\ = \dfrac{9}{{3 + 1 - \dfrac{1}{{b + 1}} + 1 - \dfrac{1}{{c + 1}} + 1 - \dfrac{1}{{a + 1}}}}\\ = \dfrac{9}{{6 - \left( {\dfrac{1}{{a + 1}} + \dfrac{1}{{b + 1}} + \dfrac{1}{{c + 1}}} \right)}}\end{array}\)
Áp dụng (*) ta có:
\(\begin{array}{l}\dfrac{1}{{a + 1}} + \dfrac{1}{{b + 1}} + \dfrac{1}{{c + 1}}\\ \ge \dfrac{{{{\left( {1 + 1 + 1} \right)}^2}}}{{a + 1 + b + 1 + c + 1}}\\ = \dfrac{{{3^2}}}{{3 + 3}} = \dfrac{3}{2}\end{array}\)
\( \Rightarrow P \ge \dfrac{9}{{6 - \dfrac{3}{2}}} = 2 \Rightarrow P \ge 2\)
Dấu “=” xảy ra khi \(a = b = c = 1\).
Vậy \(\dfrac{{{a^2}\left( {b + 1} \right)}}{{a + b + ab}} + \dfrac{{{b^2}\left( {c + 1} \right)}}{{b + c + bc}} + \dfrac{{{c^2}\left( {a + 1} \right)}}{{c + a + ca}} \ge 2\)
HẾT
Loigiaihay.com
- Giải đề thi học kì 2 toán lớp 9 năm 2020 - 2021 PGD quận Cầu Giấy
- Đề thi học kì 2 môn toán lớp 9 năm 2019 - 2020 trường THCS Hoàng Văn Thụ
- Đề thi học kì 2 môn toán lớp 9 năm 2019 - 2020 PGD quận Hà Đông
- Đề thi học kì 2 toán lớp 9 năm 2019 - 2020 PGD quận Thanh Xuân
- Giải đề thi học kì 2 toán lớp 9 năm 2019 - 2020 PGD quận Ba Đình
>> Xem thêm
Các bài khác cùng chuyên mục












Danh sách bình luận