Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Đề ôn tập học kì 1 – Có đáp án và lời giải

Đề số 14 - Đề kiểm tra học kì 1 - Toán 9

Tải về

Đáp án và lời giải chi tiết Đề số 14 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9

Lựa chọn câu để xem lời giải nhanh hơn

Đề bài

Câu 1 (2,0 điểm):

a) Tính: \(3\sqrt {16}  + 5\sqrt {36} \)

b) Chứng minh rằng: với \(x > 0\) và \(x \ne 1\) thì \(\dfrac{{\sqrt x }}{{\sqrt x  - 1}} - \dfrac{1}{{x - \sqrt x }} = \dfrac{{\sqrt x  + 1}}{{\sqrt x }}\)

Câu 2 (2,5 điểm)Cho hàm số \(y = (2m + 1)x - 6\) có đồ thị \((d)\).

a) Với giá trị nào của \(m\) thì hàm số nghịch biến trên \(R\).

b) Tìm \(m\) để đồ thị hàm số \((d)\) đã cho đi qua điểm \(A(1;\,\,2)\).

c) Vẽ \((d)\) khi \(m =  - 2\).

Câu 3 (1,5 điểm):

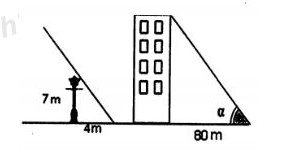
Một cột đèn cao \(7m\) có bóng trên mặt đất dài \(4m\). Gần đó có một tòa nhà cao tầng có bóng trên mặt đất dài \(80m\) (hình vẽ). Em hãy cho biết tòa nhà đó có bao nhiêu tầng, biết rằng mỗi tầng cao \(2m\).

Câu 4 (1,5 điểm):

Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) (\(H\) thuộc \(BC\)). Biết \(\angle ACB = {60^0},\,\,CH = a\). Tính độ dài \(AB\) và \(AC\) theo \(a\).

Câu 5 (3,0 điểm):

Cho tam giác \(ABC\) vuông tại \(A\,\,(AB < AC)\). Vẽ đường tròn tâm \(O\) đường kính \(AC\) cắt cạnh \(BC\) tại \(D\,\,(D \ne C)\). Gọi \(H\) và \(K\) lần lượt là trung điểm của \(AD\) và \(DC.\) Tia \(OH\) cắt cạnh \(AB\) tại \(E\) . Chứng minh:

a) \(AD\) là đường cao của tam giác \(ABC\).

b) \(DE\) là tiếp tuyến của đường tròn \((O)\).

c) Tứ giác \(OHDK\) là hình chữ nhật.

LG bài 1

Lời giải chi tiết:

a)  \(3\sqrt {16}  + 5\sqrt {36}  = 3.4 + 5.6 = 12 + 30 = 42\)

b) Với \(x > 0\) và \(x \ne 1\) ta có:

\(\begin{array}{l}\;\;\;\dfrac{{\sqrt x }}{{\sqrt x  - 1}} - \dfrac{1}{{x - \sqrt x }} \\= \dfrac{{\sqrt x }}{{\sqrt x  - 1}} - \dfrac{1}{{\sqrt x \left( {\sqrt x  - 1} \right)}} \\= \dfrac{{\sqrt x .\sqrt x }}{{\sqrt x \left( {\sqrt x  - 1} \right)}} - \dfrac{1}{{\sqrt x \left( {\sqrt x  - 1} \right)}}\\ = \dfrac{{x - 1}}{{\sqrt x \left( {\sqrt x  - 1} \right)}}\\ = \dfrac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}{{\sqrt x \left( {\sqrt x  - 1} \right)}}\\ = \dfrac{{\sqrt x  + 1}}{{\sqrt x }}\end{array}\)

Vậy với \(x > 0\) và \(x \ne 1\) thì \(\dfrac{{\sqrt x }}{{\sqrt x  - 1}} - \dfrac{1}{{x - \sqrt x }} = \dfrac{{\sqrt x  + 1}}{{\sqrt x }}\).

LG bài 2

Lời giải chi tiết:

a) Hàm số bậc nhất \(y = (2m + 1)x - 6\)nghịch biến trên \(R\) khi \(2m + 1 < 0\)

\( \Leftrightarrow 2m <  - 1\,\, \Leftrightarrow m < \dfrac{{ - 1}}{2}\)

b) Đồ thị hàm số \(y = (2m + 1)x - 6\)đi qua điểm \(A(1\,;\,\,2)\,\,\)

\(\begin{array}{l} \Leftrightarrow 2 = (2m + 1).1 - 6\\ \Leftrightarrow 2 = 2m + 1 - 6\,\,\\ \Leftrightarrow 2m = 7\,\,\\ \Leftrightarrow m = \dfrac{7}{2}.\end{array}\)

c) Khi \(m =  - 2\) ta có \(y =  - 3x - 6\).

Cho \(x = 0\,\, \Rightarrow y =  - 6\,\,\,\,;\,  y = 0 \Rightarrow x =  - 2\)

Đồ thị hàm số \(y =  - 3x - 6\) đi qua \(2\) điểm \(A\,( - 2\,;\,\,0);\,\,B\,(0\,;\,\, - 6)\)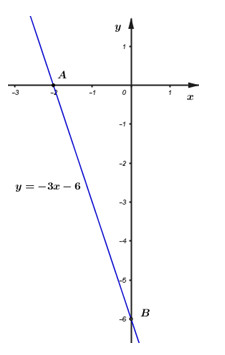

LG bài 3

Lời giải chi tiết:

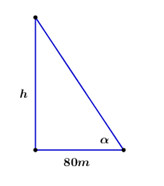
\(\Delta ACH\) vuông tại \(H\) có:

\(\cos C = \dfrac{{CH}}{{AC}}\,\,\, \)\(\Rightarrow AC = \dfrac{{CH}}{{\cos C}} = \dfrac{a}{{\cos {{60}^0}}} = \dfrac{a}{{\dfrac{1}{2}}} = 2a\)

\(\Delta ABC\) có \(AB = AC.\tan C = 2a.\tan {60^0} = 2\sqrt 3 a\)

LG bài 4

Lời giải chi tiết:

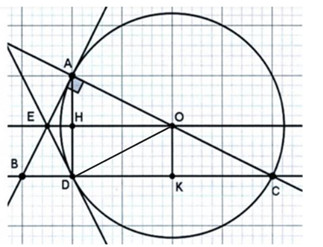
a) Ta có: \(\Delta ADC\) nội tiếp đường tròn \((O)\) đường kính \(AC\)

\( \Rightarrow \Delta ADC\) vuông tại \(D\)

\( \Rightarrow AD \bot BC\) tại \(D\)

\( \Rightarrow AD\) là đường cao của tam giác \(ABC\)

b) Ta có \(\Delta AOD\)cân tại \(O\,\,(OA = OD = R)\).

Mà \(OH\) là đường trung tuyến (\(H\) là trung điểm của \(AD\))

\( \Rightarrow OH\) là đường phân giác của \(\angle AOD\)

\( \Rightarrow \angle AOH = \angle DOH\)

Xét \(\Delta AOE\) và \(\Delta DOE\) ta có:

\(\begin{array}{l}EO\;chung\\\angle DOE = \angle AOE\;\;\left( {cmt} \right)\\OA = OD\;\left( { = R} \right)\\ \Rightarrow \Delta AOE = \Delta DOE\,\,(c - g - c).\end{array}\)

\( \Rightarrow \angle EAO = \angle EDO\)(hai góc tương ứng)

Mà \(\angle EAO = {90^0}\,\,(\Delta ABC\) vuông tại \(A\))\( \Rightarrow \angle EDO = {90^0}\,\,\, \Rightarrow ED \bot OD\)

Mà \(D\) thuộc \((O)\,\, \Rightarrow DE\) là tiếp tuyến của đường tròn \((O)\).

c) Ta có \(H\) là trung điểm của dây cung \(AD\) của \((O)\)

\( \Rightarrow OH \bot AD\) tại \(H\) (đường kính – dây cung)

Hay \(\angle OHD = {90^0}\)

Ta có \(K\) là trung điểm của dây cung \(DC\) của \((O)\)

\( \Rightarrow OK \bot DC\) tại \(K\) (đường kính – dây cung)

Hay \(\angle OKD = {90^0}\)

Mà \(AD \bot DC \Rightarrow \angle HDO = {90^0}\)

Xét tứ giác \(OHDK\) ta có: \(\angle OHD = \angle HDK = \angle DKO = {90^0}\)

\( \Rightarrow \) Tứ giác \(OHDK\) là hình chữ nhật. (dhnb)

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 9 tại Tuyensinh247.com

 Loigiaihay.com

 


Bình chọn:
4 trên 3 phiếu
Tải về
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store