Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Đề ôn tập học kì 1 – Có đáp án và lời giải

Đề số 13 - Đề kiểm tra học kì 1 - Toán 9

Tải về

Đáp án và lời giải chi tiết Đề số 13 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9

Lựa chọn câu để xem lời giải nhanh hơn

Đề bài

Câu 1 (3,0 điểm):

a) Nêu điều kiệnđể \(\sqrt A \) có nghĩa.

Áp dụng: Tìm điều kiện của \(x\) để \(\sqrt {3x - 7} \) có nghĩa.

b) Tính: \(\dfrac{1}{2}\sqrt {48}  - 2\sqrt {75}  + \dfrac{{\sqrt {33} }}{{\sqrt {11} }}.\)

c) Rút gọn biểu thức: \(P = \left( {\dfrac{{x\sqrt x  - 1}}{{x - \sqrt x }} - \dfrac{{x\sqrt x  + 1}}{{x + \sqrt x }}} \right):\left[ {\dfrac{{2\left( {x - 2\sqrt x  + 1} \right)}}{{x - 1}}} \right]\)   (với \(x > 0\)và \(x \ne 1\))

Câu 2 (3 điểm):

Cho hàm số \(y = 2x - 2\).

a) Hàm số đã cho đồng biến hay nghịch biến trên \(\mathbb{R}\). Vì sao?

b) Vẽ đồ thị hàm số \(y = 2x - 2\).

c) Với giá trị nào của \(m\) thì đường thẳng \(y = (m - 1)x + 3\,\,\,\,\,(m \ne 1)\) song song với đường thẳng \(y = 2x - 2\).

Câu 3 (1,0 điểm):

Giải hệ phương trình: \(\left\{ \begin{array}{l}3x + y = 3\\2x - y = 7\end{array} \right.\)

Câu 4 (1,0 điểm):

Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\), biết \(BH = 9cm,\,\,CH = 25cm\). Tính \(AH\).

Câu 5 (1 điểm):

Cho đường tròn \((O)\), điểm \(A\) nằm bên ngoài đường tròn. Kẻ các tiếp tuyến \(AM,AN\) với đường tròn (\(M,N\) là các tiếp điểm).

a) Chứng minh rằng \(OA \bot MN\).

b) Vẽ đường kính \(NOC\). Chứng minh rằng MC// AO.

LG bài 1

Lời giải chi tiết:

a) Điều kiện để \(\sqrt A \) có nghĩa là \(A \ge 0\).

Áp dụng: \(\sqrt {3x - 7} \) có nghĩa khi \(3x - 7 \ge 0\)\( \Leftrightarrow 3x \ge 7\,\, \Leftrightarrow x \ge \dfrac{7}{3}\)

Vậy với \(x \ge \dfrac{7}{3}\) thì \(\sqrt {3x - 7} \) có nghĩa.

b) Ta có:

\(\begin{array}{l}\dfrac{1}{2}\sqrt {48}  - 2\sqrt {75}  + \dfrac{{\sqrt {33} }}{{\sqrt {11} }} = \dfrac{1}{2}\sqrt {16.3}  - 2\sqrt {25.3}  + \sqrt {\dfrac{{33}}{{11}}} \\ = \dfrac{1}{2}.4\sqrt 3  - 2.5\sqrt 3  + \sqrt 3 \\ = 2\sqrt 3  - 10\sqrt 3  + \sqrt 3 \\ =  - 7\sqrt 3 \end{array}\)

c) Điều kiện: \(x > 0,\;\;x \ne 1.\)

\(\begin{array}{l}P = \left( {\dfrac{{x\sqrt x  - 1}}{{x - \sqrt x }} - \dfrac{{x\sqrt x  + 1}}{{x + \sqrt x }}} \right):\left[ {\dfrac{{2\left( {x - 2\sqrt x  + 1} \right)}}{{x - 1}}} \right]\\ = \left[ {\dfrac{{{{\left( {\sqrt x } \right)}^3} - {1^3}}}{{\sqrt x \left( {\sqrt x  - 1} \right)}} - \dfrac{{{{\left( {\sqrt x } \right)}^3} + {1^3}}}{{\sqrt x \left( {\sqrt x  + 1} \right)}}} \right]:\left[ {\dfrac{{2{{\left( {\sqrt x  - 1} \right)}^2}}}{{{{\left( {\sqrt x } \right)}^2} - 1}}} \right]\\ = \left[ {\dfrac{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}}{{\sqrt x \left( {\sqrt x  - 1} \right)}} - \dfrac{{\left( {\sqrt x  + 1} \right)\left( {x - \sqrt x  + 1} \right)}}{{\sqrt x \left( {\sqrt x  + 1} \right)}}} \right]:\left[ {\dfrac{{2{{\left( {\sqrt x  - 1} \right)}^2}}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}} \right]\\ = \left( {\dfrac{{\left( {x + \sqrt x  + 1} \right)}}{{\sqrt x }} - \dfrac{{\left( {x - \sqrt x  + 1} \right)}}{{\sqrt x }}} \right):\dfrac{{2\left( {\sqrt x  - 1} \right)}}{{\sqrt x  + 1}}\\ = \dfrac{{2\sqrt x }}{{\sqrt x }}.\dfrac{{\sqrt x  + 1}}{{2\left( {\sqrt x  - 1} \right)}} = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}}\end{array}\)

LG bài 2

Lời giải chi tiết:

a) Hàm số đã cho đồng biến trên \(\mathbb{R}\) vì \(a = 2 > 0\).

b) Vẽ đồ thị hàm số \(y = 2x - 2\)

Cho \(x = 0 \Rightarrow y =  - 2\), ta được điểm \((0; - 2)\) thuộc đường thẳng \(y = 2x - 2\);

\(y = 0 \Rightarrow x = 1\), ta được điểm \((1;0)\) thuộc đường thẳng \(y = 2x - 2\).

Vậy đồ thị hàm số \(y = 2x - 2\)là đường thẳng đi qua 2 điểm \(\left( {0; - 2} \right),\;\left( {1;\;0} \right).\;\)

Đồ thị hàm số như hình vẽ bên: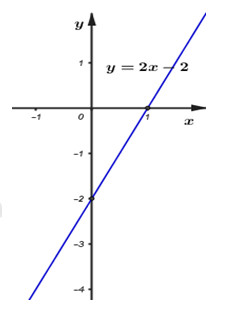 

 

c) Đường thẳng \(y = (m - 1)x + 3\,\,(m \ne 1)\) song song với đường thẳng \(y = 2x - 2\)

\(\begin{array}{l} \Leftrightarrow m - 1 = 2\\ \Leftrightarrow m = 3\end{array}\) (vì \(3 \ne  - 2\))

LG bài 3

Lời giải chi tiết:

\(\begin{array}{l}\;\;\;\;\;\left\{ \begin{array}{l}3x + y = 3\\2x - y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3 - 3x\\2x - (3 - 3x) = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3 - 3x\\2x - 3 + 3x = 7\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 3 - 3x\\5x = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3 - 3.2\\x = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y =  - 3\\x = 2\end{array} \right.\end{array}\)

Vậy hệ phương trình đã cho có nghiệm là \((x;y) = (2; - 3).\)

LG bài 4

Lời giải chi tiết:

 

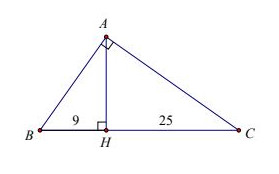
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:

\(\begin{array}{l}A{H^2} = BH.CH\\ \Rightarrow AH = \sqrt {BH.CH}  = \sqrt {9.25}  = \sqrt {225} \\ \Rightarrow AH = 15cm\end{array}\)

LG bài 5

Lời giải chi tiết:

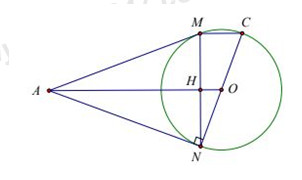
a) Ta có:

\(AM = AN,\,\,\,AO\) là tia phân giác của góc \(A\) (tính chất của hai

tiếp tuyến cắt nhau)

\( \Rightarrow \Delta AMN\) cân tại \(A\), có \(AO\) là tia phân giác của góc \(A\)

\( \Rightarrow AO\) là đường cao ứng với cạnh \(MN\)

\( \Rightarrow AO \bot MN\;\;\left( {dpcm} \right).\)

b) Gọi \(H\) là giao điểm của \(MN\) và \(OA\), có \(AO \bot MN\)(tính chất 2 tiếp tuyến cắt nhau).

\( \Rightarrow MH = HN\) (quan hệ vuông góc giữa đường kính và dây)

MÀ \(CO = ON\) (cùng bán kính \((O)\))

\( \Rightarrow HO\) là đường trung bình của tam giác \(MNC\)

\( \Rightarrow HO//MC,\) do đó \(MC//AO.\)

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 9 tại Tuyensinh247.com

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Tải về
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store