Đề số 11 - Đề kiểm tra học kì 1 - Toán 9

Đề bài

Câu 1 (2,5 điểm):Cho hai biểu thức$A = \frac{{x - 2\sqrt x  + 9}}{{\sqrt x  - 3}}$và $B = \frac{{\sqrt x  + 3}}{{\sqrt x  - 3}} + \frac{{\sqrt x }}{{\sqrt x  + 3}} - \frac{{x + 9}}{{x - 9}}$với $x > 0,\,\,x \ne 9$

1) Tính giá trị của biểu thức A khi $x = 3$

2) Chứng minh $B = \frac{{\sqrt x }}{{\sqrt x  - 3}}$

3) So sánh $\frac{A}{B}$ và 4.

Câu 2 (2,5 điểm):Cho hàm số $y = \left( {m + 1} \right)x + m$ (với $m \ne  - 1$có đồ thị là đường thẳng $\left( d \right)$

1) Tìm giá trị của m để đường thẳng $\left( d \right)$ cắt trục tung tại điểm có tung độ là 1

2) Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng $\left( d \right)$ với giá trị m tìm được ở câu 1

3) Tìm giá trị của m để đường thẳng $\left( d \right)$ cắt đường thẳng $y = 3x + 2$ tại một điểm nằm trên trục hoành

Câu 3 (1,0 điểm):

Giải hệ phương trình:  $\left\{ \begin{array}{l}x + \left( {\sqrt 2  - 1} \right)y = 1\\\left( {\sqrt 2  + 1} \right)x - y = \sqrt 2  + 1\end{array} \right.$

Câu 4 (3,5 điểm):Cho đường tròn $\left( {O;R} \right)$ và một điểm H cố định nằm ngoài đường tròn. Qua H kẻ đường thẳng d vuông góc với đoạn thẳng OH. Từ một điểm S bất kì trên đường thẳng d kẻ hai tiếp tuyến SA, SB với đường tròn $\left( {O;R} \right)$ (A, B là tiếp điểm). Gọi M,N lần lượt là giao điểm của đoạn thẳng SO với đoạn thẳng AB và với đường tròn $\left( {O;R} \right)$.

1) Chứng minh bốn điếm S, A, O, B cùng nằm trên một đường tròn

2) Chứng minh $OM.OS = {R^2}$

3) Chứng minh N là tâm đường tròn nội tiếp tam giác SAB

4) Khi điểm S di chuyển trên đường thẳng d thì điểm M di chuyển trên đường nào? Tại sao?

Câu 5 (0,5 điểm):Cho ba số thực dương $x,\,y,\,z$ thỏa mãn $x + y + z = 1$

Chứng minh rằng $P = \frac{{5{y^3} - {x^3}}}{{yx + 3{y^2}}} + \frac{{5{z^3} - {y^3}}}{{zy + 3{z^2}}} + \frac{{5{x^3} - {z^3}}}{{xz + 3{x^2}}} \le 1$

LG bài 1

Lời giải chi tiết:

Cho hai biểu thức $A = \frac{{x - 2\sqrt x  + 9}}{{\sqrt x  - 3}}$ và $B = \frac{{\sqrt x  + 3}}{{\sqrt x  - 3}} + \frac{{\sqrt x }}{{\sqrt x  + 3}} - \frac{{x + 9}}{{x - 9}}$ với $x > 0,\,\,x \ne 9$

1) Tính giá trị của biểu thức A khi $x = 3$

Khi $x = 3$thì $A = \frac{{3 - 2\sqrt 3  + 9}}{{\sqrt 3  - 3}} = \frac{{\left( { - 5 - \sqrt 3 } \right)\left( {\sqrt 3  - 3} \right)}}{{\sqrt 3  - 3}} =  - 5 - \sqrt 3$

2) Chứng minh $B = \frac{{\sqrt x }}{{\sqrt x  - 3}}$

$\begin{array}{l}B = \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 3}} + \dfrac{{\sqrt x }}{{\sqrt x  + 3}} - \dfrac{{x + 9}}{{x - 9}} \\\;\;\;= \dfrac{{{{\left( {\sqrt x  + 3} \right)}^2} + \sqrt x \left( {\sqrt x  - 3} \right) - \left( {x + 9} \right)}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\\;\;\; = \dfrac{{x + 6\sqrt x  + 9 + x - 3\sqrt x  - x - 9}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}} \\\;\;\;= \dfrac{{x + 3\sqrt x }}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\\;\;\; = \dfrac{{\sqrt x \left( {\sqrt x  + 3} \right)}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}} \\\;\;\;= \dfrac{{\sqrt x }}{{\sqrt x  - 3}}.\end{array}$

3) So sánh $\frac{A}{B}$ và 4.

$\begin{array}{l}\frac{A}{B} = \frac{{x - 2\sqrt x  + 9}}{{\sqrt x  - 3}}.\frac{{\sqrt x  - 3}}{{\sqrt x }} = \frac{{x - 2\sqrt x  + 9}}{{\sqrt x }}\\\;\;\; = \sqrt x  - 2 + \frac{9}{{\sqrt x }}.\end{array}$

Áp dụng bất đẳng thức Cô-si cho hai số không âm $\sqrt x$và $\frac{9}{{\sqrt x }}$ ta có: $\sqrt x  + \frac{9}{{\sqrt x }} \ge 2.\sqrt {\sqrt x .\frac{9}{{\sqrt x }}}  = 2.3 = 6.$

$\Rightarrow \frac{A}{B} = \left( {\sqrt x  + \frac{9}{{\sqrt x }}} \right) - 2 \ge 6 - 2 = 4.$

Dấu “=” xảy ra $\Leftrightarrow \sqrt x  = \frac{9}{{\sqrt x }} \Leftrightarrow x = 9\;\;\left( {tm} \right).$

Vậy $\frac{A}{B} \ge 4$.

LG bài 2

Lời giải chi tiết:

Cho hàm số $y = \left( {m + 1} \right)x + m$ (với $m \ne  - 1$ có đồ thị là đường thẳng $\left( d \right)$

1) Tìm giá trị của m để đường thẳng $\left( d \right)$ cắt trục tung tại điểm có tung độ là 1

Để đường thẳng $\left( d \right)$ cắt trục tung tại điểm có tung độ là 1$\Rightarrow$ Điểm $A\left( {0;1} \right)$ thuộc $\left( d \right)$

$\Rightarrow 1 = \left( {m + 1} \right)0 + m \Leftrightarrow m = 1$.

Vậy với $m = 1$đường thẳng $\left( d \right)$ cắt trục tung tại điểm có tung độ là 1.

2) Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng $\left( d \right)$ với giá trị m tìm được ở câu 1

Với $m = 1$ thì $\left( d \right):\,y = 2x + 1$

Ta có:

Cho hàm số $y = \left( {m + 1} \right)x + m$ (với $m \ne  - 1$ có đồ thị là đường thẳng $\left( d \right)$

1) Tìm giá trị của m để đường thẳng $\left( d \right)$ cắt trục tung tại điểm có tung độ là 1

Để đường thẳng $\left( d \right)$ cắt trục tung tại điểm có tung độ là 1$\Rightarrow$ Điểm $A\left( {0;1} \right)$ thuộc $\left( d \right)$

$\Rightarrow 1 = \left( {m + 1} \right)0 + m \Leftrightarrow m = 1$.

Vậy với $m = 1$đường thẳng $\left( d \right)$ cắt trục tung tại điểm có tung độ là 1.

2) Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng $\left( d \right)$ với giá trị m tìm được ở câu 1

Với $m = 1$ thì $\left( d \right):\,y = 2x + 1$

Ta có:

x	0	1
$y = 2x + 1$	1	3

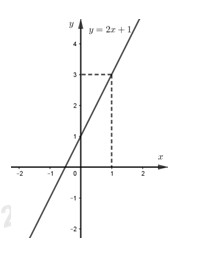
Đồ thị hàm số $\left( d \right):\,y = 2x + 1$ là đường thẳng đi qua hai điểm $\left( {0;1} \right)$ và $\left( {1;3} \right)$

3) Tìm giá trị của m để đường thẳng $\left( d \right)$ cắt đường thẳng $y = 3x + 2$ tại một điểm nằm trên trục hoành

Gọi đường thẳng $\left( d \right)$ cắt đường thẳng $y = 3x + 2$ tại một điểmB nằm trên trục hoành

$\Rightarrow$B là giao điểm của đường thẳng $y = 3x + 2$ với trục hoành $\Rightarrow \,\,B\left( { - \frac{2}{3};0} \right)$

Vì B cũng thuộc $\left( d \right)$$\Rightarrow 0 = \left( {m + 1} \right)\left( { - \frac{2}{3}} \right) + m \Leftrightarrow \frac{1}{3}m - \frac{2}{3} = 0 \Leftrightarrow m = 2$

Vậy với $m = 2$ thỏa mãn yêu cầu đề bài.

 

LG bài 3

Lời giải chi tiết:

Giải hệ phương trình:  $\left\{ \begin{array}{l}x + \left( {\sqrt 2  - 1} \right)y = 1\\\left( {\sqrt 2  + 1} \right)x - y = \sqrt 2  + 1\end{array} \right.$

$\begin{array}{l}\left\{ \begin{array}{l}x + \left( {\sqrt 2  - 1} \right)y = 1\\\left( {\sqrt 2  + 1} \right)x - y = \sqrt 2  + 1\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x = 1 - \left( {\sqrt 2  - 1} \right)y\\\left( {\sqrt 2  + 1} \right)x - y = \sqrt 2  + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1 - \left( {\sqrt 2  - 1} \right)y\\\left( {\sqrt 2  + 1} \right)\left[ {1 - \left( {\sqrt 2  - 1} \right)y} \right] - y = \sqrt 2  + 1\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x = 1 - \left( {\sqrt 2  - 1} \right)y\\\sqrt 2  + 1 - \left( {\sqrt 2  + 1} \right)\left( {\sqrt 2  - 1} \right)y - y = \sqrt 2  + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1 - \left( {\sqrt 2  - 1} \right)y\\ - y - y = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1 - \left( {\sqrt 2  - 1} \right)y\\ - 2y = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1 - \left( {\sqrt 2  - 1} \right)y\\y = 0\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 0\end{array} \right..\end{array}$

Vậy nghiệm của hệ phương trình là$\left( {x;y} \right) = \left( {1;0} \right)$

LG bài 4

Lời giải chi tiết:

Cho đường tròn $\left( {O;R} \right)$ và một điểm H cố định nằm ngoài đường tròn. Qua H kẻ đường thẳng d vuông góc với đoạn thẳng OH. Từ một điểm S bất kì trên đường thẳng d kẻ hai tiếp tuyến SA, SB với đường tròn $\left( {O;R} \right)$ (A, B là tiếp điểm). Gọi M,N lần lượt là giao điểm của đoạn thẳng SO với đoạn thẳng AB và với đường tròn $\left( {O;R} \right)$.

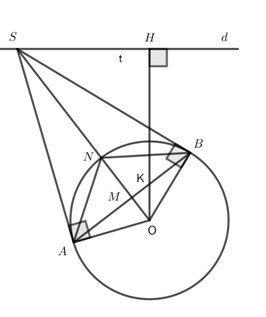
1) Chứng minh bốn điếm S, A, O, B cùng nằm trên một đường tròn

Ta có SA,SBlà hai tiếp tuyến của $\left( O \right)$$\Rightarrow \angle OAS = \angle OBS = {90^o}$

$\Rightarrow$A, Bcùng thuộc đường tròn đường kính OS

$\Rightarrow$ A, B, O, Scùng thuộc một đường tròn đường kính OS.

2)Chứng minh $OM.OS = {R^2}$

Ta có SA, SBlà hai tiếp tuyến của $\left( O \right)$ cắt nhau tại S

$\Rightarrow$$SA = SB$ và SO là phân giác $\angle ASB$  (tính chất 2 tiếp tuyến cắt nhau)

$\Rightarrow \Delta SAB$ là tam giác cân tại S.

$\Rightarrow$SO vừa là phân giác $\angle ASB$ vừa là đường trung trực của AB (tính chất tam giác cân)

$\Rightarrow SO \bot AB$ tại M.

$\Rightarrow$AMlà đường cao trong tam giác OAS

Xét tam giác OAS vuông tại A, đường cao AMta có:

$OM.OS = O{A^2} = {R^2}$(hệ thức về cạnh và đường cao trong tam giác vuông)

3) Chứng minh N là tâm đường tròn nội tiếp tam giác SAB

Có $\angle OBS = {90^o}$ ( SB là tiếp tuyến của $\left( O \right)$)$\Rightarrow \angle OBN + \angle NBS = {90^o}\,\,\,\,\,\,\left( 1 \right)$

Có  $SO \bot AB$ (chứng minh trên)$\Rightarrow$Tam giác MNB vuông tại M$\Rightarrow \angle MNB + \angle NBM = {90^o}\,\,\,\,\,\left( 2 \right)$

Có $ON = OB = R \Rightarrow$ Tam giác ONB cân tại O$\Rightarrow \angle MNB = \angle OBN$(tính chất tam giác cân) $\left( 3 \right)$

Từ $\left( 1 \right),\left( 2 \right),\left( 3 \right) \Rightarrow \angle NBS = \angle NBM$$\Rightarrow$BN là phân giác $\angle SBA$

Mặt khác SN là phân giác $\angle ASB$ (tính chất hai tiếp tuyến cắt nhau) và $SN \cap BN = \left\{ N \right\}$

$\Rightarrow$N là tâm đường tròn nội tiếp tam giác SAB.

4) Khi điểm S di chuyển trên đường thẳng d thì điểm M di chuyển trên đường nào? Tại sao?

Gọi $HO \cap AB = \left\{ K \right\}$.

Xét $\Delta OMK$ và $\Delta OHS$ có: $\angle O$chung; $\angle OMK = \angle OHS\,\,\,( = {90^o})$

$\Rightarrow \Delta OMK \sim \Delta OHS$(g.g) $\Rightarrow \frac{{OK}}{{OS}} = \frac{{OM}}{{OH}} \Rightarrow OK.OH = OM.OS = {R^2}$

Vì H cố định $\Rightarrow$OH cố định mà R cố định$\Rightarrow$OK cố định.

Mặt khác $\angle OMK = {90^o}$$\Rightarrow$M thuộc đường tròn đường kính OK cố định.

Vậy khi điểm S di chuyển trên đường thẳng d thì điểm M di chuyển trên đường tròn đường kính OK cố định.

LG bài 5

Lời giải chi tiết:

Cho ba số thực dương $x,\,y,\,z$ thỏa mãn $x + y + z = 1$

Chứng minh rằng $P = \frac{{5{y^3} - {x^3}}}{{yx + 3{y^2}}} + \frac{{5{z^3} - {y^3}}}{{zy + 3{z^2}}} + \frac{{5{x^3} - {z^3}}}{{xz + 3{x^2}}} \le 1$

Với $x,y,z > 0$ ta có :  $\frac{{5{y^3} - {x^3}}}{{yx + 3{y^2}}} \le 2y - x \Leftrightarrow 5{y^3} - {x^3} \le  - {x^2}y + 6{y^3} - x{y^2}$

$\Leftrightarrow {x^3} + {y^3} - xy\left( {x + y} \right) \ge 0 \Leftrightarrow \left( {x + y} \right){\left( {x - y} \right)^2} \ge 0$luôn đúng với mọi $x,\;y > 0.$

$\Rightarrow \frac{{5{y^3} - {x^3}}}{{yx + 3{y^2}}} \le 2y - x$đúng với $x,y,z > 0$

Tương tự ta được $\frac{{5{z^3} - {y^3}}}{{zy + 3{z^2}}} \le 2z - y\,;\,\,\frac{{5{x^3} - {z^3}}}{{xz + 3{x^2}}} \le 2x - z$

$\Rightarrow P = \frac{{5{y^3} - {x^3}}}{{yx + 3{y^2}}} + \frac{{5{z^3} - {y^3}}}{{zy + 3{z^2}}} + \frac{{5{x^3} - {z^3}}}{{xz + 3{x^2}}} \le 2y - x + 2z - y + 2x - z = x + y + z = 1$

Dấu ‘=’ xảy ra khi $\left\{ \begin{array}{l}x = y = z\\x + y + z = 1\end{array} \right. \Leftrightarrow x = y = z = \frac{1}{3}$

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 9 tại Tuyensinh247.com

Loigiaihay.com