Đề số 10 - Đề kiểm tra học kì 1 - Toán 9

Đề bài

Câu 1 (2,0 điểm): Hãy tính giá trị của:

a) \(M = \left( {2\sqrt {300}  + 3\sqrt {48}  - 4\sqrt {75} } \right):\sqrt 3 \) ;

b) \(N = \sqrt {{{\left( {\sqrt 3  - 2} \right)}^2}}  + \sqrt {4 - 2\sqrt 3 } \) ;

c) \(P = \dfrac{2}{{\sqrt 3  + 1}} - \dfrac{1}{{\sqrt 3  - 2}} + \dfrac{{12}}{{\sqrt 3  + 3}}\) ;

Câu 2 (2,0 điểm): Cho các biểu thức:

\(A = 1 - \dfrac{{\sqrt x }}{{1 + \sqrt x }}\)  và  \(B = \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 2}} + \dfrac{{\sqrt x  + 2}}{{3 - \sqrt x }} + \dfrac{{\sqrt x  + 2}}{{x - 5\sqrt x  + 6}}\)  với \(x \ge 0,\,\,x \ne 4,\,\,x \ne 9.\)

a) Hãy tính giá trị của A khi \(x = 16\).

b) Rút gọn B.

c) Xét biểu thức \(T = \dfrac{A}{B}\) . Hãy tìm giá trị nhỏ nhất của T.

Câu 3 (2,0 điểm): Cho hàm số \(y = \left( {2 - m} \right)x + m + 1\) (với m là tham số và \(m \ne 2\)) có đồ thị là đường thẳng \(\left( d \right).\)

a) Khi \(m = 0\), hãy vẽ \(\left( d \right)\) trên hệ trục tọa độ \(Oxy\).

b) Tìm m để \(\left( d \right)\) cắt đường thẳng \(y = 2x - 5\) tại điểm có hoành độ bằng 2.

c) Tìm m để \(\left( d \right)\) cùng với các trục tọa độ \(Ox,\,\,Oy\) tạo thành một tam giác có diện tích bằng 2.

Câu 4 (3,5 điểm): Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài \(\left( O \right)\). Từ A kẻ hai tiếp tuyến AB, AC với \(\left( O \right)\) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC.

a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.

b) Chứng minh OA là đường trung trực của BC.

c) Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với \(\left( O \right)\) (E không trùng với D). Chứng minh \(\dfrac{{DE}}{{BE}} = \dfrac{{BD}}{{BA}}\).

d) Tính số đo góc HEC.

Câu 5 (0,5 điểm): Cho \(x > 0,\,\,y > 0\) thỏa mãn \(xy = 6\). Tìm giá trị nhỏ nhất của biểu thức:

\(Q = \dfrac{2}{x} + \dfrac{3}{y} + \dfrac{6}{{3x + 2y}}\) .

LG bài 1

Lời giải chi tiết:

a) \(M = \left( {2\sqrt {300}  + 3\sqrt {48}  - 4\sqrt {75} } \right):\sqrt 3 \)

\(\begin{array}{l}M = \left( {2\sqrt {300}  + 3\sqrt {48}  - 4\sqrt {75} } \right):\sqrt 3  = \left( {2.10\sqrt 3  + 3.4\sqrt 3  - 4.5\sqrt 3 } \right):\sqrt 3 \\\,\,\,\,\,\,\, = \left( {20\sqrt 3  + 12\sqrt 3  - 20\sqrt 3 } \right):\sqrt 3  = 12\sqrt 3 :\sqrt 3  = 12\end{array}\)

b) \(N = \sqrt {{{\left( {\sqrt 3  - 2} \right)}^2}}  + \sqrt {4 - 2\sqrt 3 } \) ;

\(\begin{array}{l}N = \sqrt {{{\left( {\sqrt 3  - 2} \right)}^2}}  + \sqrt {4 - 2\sqrt 3 }  \\\;\;\;= \left| {\sqrt 3  - 2} \right| + \sqrt {{{\left( {\sqrt 3  - 1} \right)}^2}}  = 2 - \sqrt 3  + \left| {\sqrt 3  - 1} \right|\\\,\,\,\,\,\, = 2 - \sqrt 3  + \sqrt 3  - 1 = 1\end{array}\)

c) \(P = \dfrac{2}{{\sqrt 3  + 1}} - \dfrac{1}{{\sqrt 3  - 2}} + \dfrac{{12}}{{\sqrt 3  + 3}}\) ;

\(\begin{array}{l}P = \dfrac{2}{{\sqrt 3  + 1}} - \dfrac{1}{{\sqrt 3  - 2}} + \dfrac{{12}}{{\sqrt 3  + 3}}\\ = \dfrac{{2\left( {\sqrt 3  - 1} \right)}}{{\left( {\sqrt 3  + 1} \right)\left( {\sqrt 3  - 1} \right)}} - \dfrac{{1\left( {\sqrt 3  + 2} \right)}}{{\left( {\sqrt 3  - 2} \right)\left( {\sqrt 3  + 2} \right)}} + \dfrac{{12\left( {3 - \sqrt 3 } \right)}}{{\left( {3 + \sqrt 3 } \right)\left( {3 - \sqrt 3 } \right)}}\\= \dfrac{{2\left( {\sqrt 3  - 1} \right)}}{2} - \dfrac{{\sqrt 3  + 2}}{{ - 1}} + \dfrac{{12\left( {3 - \sqrt 3 } \right)}}{6}\\ = \sqrt 3  - 1 + \sqrt 3  + 2 + 2\left( {3 - \sqrt 3 } \right) = 7\end{array}\)

LG bài 2

Lời giải chi tiết:

Câu 2: Cho các biểu thức:

\(A = 1 - \dfrac{{\sqrt x }}{{1 + \sqrt x }}\)  và  \(B = \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 2}} + \dfrac{{\sqrt x  + 2}}{{3 - \sqrt x }} + \dfrac{{\sqrt x  + 2}}{{x - 5\sqrt x  + 6}}\)  với \(x \ge 0,\,\,x \ne 4,\,\,x \ne 9.\)

a) Hãy tính giá trị của A khi \(x = 16\).

Tại \(x = 16\)thì \(A = 1 - \dfrac{{\sqrt {16} }}{{1 + \sqrt {16} }} = 1 - \dfrac{4}{{1 + 4}} = 1 - \dfrac{4}{5} = \dfrac{1}{5}\)

b) Rút gọn B.

\(\begin{array}{l}B = \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 2}} + \dfrac{{\sqrt x  + 2}}{{3 - \sqrt x }} + \dfrac{{\sqrt x  + 2}}{{x - 5\sqrt x  + 6}}\\\;\;\; = \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 2}} - \dfrac{{\sqrt x  + 2}}{{\sqrt x  - 3}} + \dfrac{{\sqrt x  + 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\\\;\;\; = \dfrac{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right) - \left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right) + \sqrt x  + 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\\\,\,\,\,\, = \dfrac{{x - 9 - x + 4 + \sqrt x  + 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}} = \dfrac{{\sqrt x  - 3}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}} = \dfrac{1}{{\sqrt x  - 2}}\end{array}\)

c) Xét biểu thức \(T = \dfrac{A}{B}\) . Hãy tìm giá trị nhỏ nhất của T.

\(A = 1 - \dfrac{{\sqrt x }}{{1 + \sqrt x }} = \dfrac{{1 + \sqrt x  - \sqrt x }}{{1 + \sqrt x }} = \dfrac{1}{{1 + \sqrt x }}\)

\(T = \dfrac{A}{B} = \dfrac{1}{{1 + \sqrt x }}:\dfrac{1}{{\sqrt x  - 2}} = \dfrac{{\sqrt x  - 2}}{{1 + \sqrt x }} = \dfrac{{\sqrt x  + 1 - 3}}{{1 + \sqrt x }} = 1 - \dfrac{3}{{1 + \sqrt x }}\)

Do \(x \ge 0 \Rightarrow \sqrt x  \ge 0 \Rightarrow \dfrac{3}{{1 + \sqrt x }} \le \dfrac{3}{1} = 3 \Rightarrow T = 1 - \dfrac{3}{{1 + \sqrt x }} \ge 1 - 3 =  - 2\)

Dấu bằng xảy ra khi \(x = 0\)

Vậy \(Min\;T =  - 2\) khi \(x = 0.\)

LG bài 3

Lời giải chi tiết:

Câu 3: Cho hàm số \(y = \left( {2 - m} \right)x + m + 1\) (với m là tham số và \(m \ne 2\)) có đồ thị là đường thẳng \(\left( d \right).\)

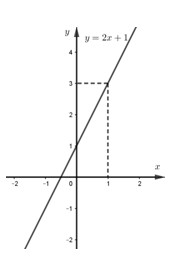
a) Khi \(m = 0\), hãy vẽ \(\left( d \right)\) trên hệ trục tọa độ \(Oxy\).

Khi\(m = 0\) thì \(\left( d \right):\;\;y = 2x + 1\)

Đồ thị của đường thẳng \(\left( d \right)\) đi qua 2 điểm \(\left( {0;1} \right),\,\,\,\left( {1;3} \right).\)

b) Tìm m để \(\left( d \right)\) cắt đường thẳng \(y = 2x - 5\) tại điểm có hoành độ bằng 2.

Phương trình hoành độ giao điểm của \(\left( d \right)\) và đường thẳng \(y = 2x - 5\) là

\(\left( {2 - m} \right)x + m + 1 = 2x - 5 \Leftrightarrow mx = m + 6\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)

Để \(\left( d \right)\) cắt đường thẳng \(y = 2x - 5\) tại điểm có hoành độ bằng 2 thì \(x = 2\)  là nghiệm của phương trình \(\left( 1 \right)\) hay \(2m = m + 6 \Leftrightarrow m = 6.\)

Vậy với \(m = 6\) thỏa mãn yêu cầu đề bài.

c) Tìm m để \(\left( d \right)\) cùng với các trục tọa độ \(Ox,\,\,Oy\) tạo thành một tam giác có diện tích bằng 2.

Gọi A và B là giao điểm của \(\left( d \right)\) lần lượt với hai trục tọa độ Ox, Oy.

Tọa độ điểm A thỏa mãn \(\left\{ \begin{array}{l}y = \left( {2 - m} \right)x + m + 1\\y = 0\end{array} \right. \Leftrightarrow x = \dfrac{{m + 1}}{{m - 2}} \)

\(\Rightarrow A\left( {\dfrac{{m + 1}}{{m - 2}};0} \right) \Rightarrow OA = \left| {\dfrac{{m + 1}}{{m - 2}}} \right|\)

Tọa độ điểm B thỏa mãn \(\left\{ \begin{array}{l}y = \left( {2 - m} \right)x + m + 1\\x = 0\end{array} \right. \Leftrightarrow y = m + 1\)

\(\Rightarrow B\left( {0;m + 1} \right) \Rightarrow OB = \left| {m + 1} \right|\)

\({S_{\Delta OAB}} = 2 \Leftrightarrow \dfrac{{OA.OB}}{2} = 2\)

\(\Leftrightarrow \left| {\dfrac{{m + 1}}{{m - 2}}} \right|.\left| {m + 1} \right| = 4\)

\(\Leftrightarrow {\left( {m + 1} \right)^2} = 4\left| {m - 2} \right|\)

Trường hợp 1: \(m > 2 \Rightarrow pt \Leftrightarrow {\left( {m + 1} \right)^2} = 4\left( {m - 2} \right) \Leftrightarrow {m^2} - 2m + 9 = 0\) vô nghiệm.

Trường hợp 2: \(m < 2 \Rightarrow pt \Leftrightarrow {\left( {m + 1} \right)^2} =  - 4\left( {m - 2} \right) \Leftrightarrow {m^2} + 6m - 7 = 0 \)

\(\Leftrightarrow \left[ \begin{array}{l}m = 1\;\;\;\left( {tm} \right)\\m =  - 7\;\;\left( {tm} \right)\end{array} \right.\)

Vậy với \(m = 1\) hoặc \(m =  - 7\) thỏa mãn yêu cầu đề bài.

LG bài 4

Lời giải chi tiết:

Câu 4: Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài \(\left( O \right)\). Từ A kẻ hai tiếp tuyến AB, AC với \(\left( O \right)\) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC.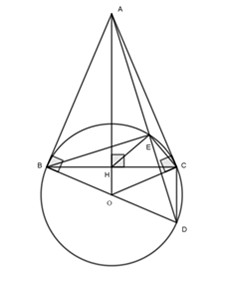

a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.

Ta có AB, AC là hai tiếp tuyến của \(\left( O \right)\)\( \Rightarrow \angle OBA = \angle OCA = {90^o}\)

\( \Rightarrow \)B, C cùng thuộc đường tròn đường kính OA

\( \Rightarrow \) A, B, O, C cùng thuộc một đường tròn đường kính OA. (đpcm)

b) Chứng minh OA là đường trung trực của BC.

Ta có AB, AC là hai tiếp tuyến của \(\left( O \right)\) cắt nhau tại A

\( \Rightarrow \)\(AB = AC\) và AO là phân giác \(\angle BAC\)  (tính chất 2 tiếp tuyến cắt nhau)

\( \Rightarrow \Delta ABC\) là tam giác cân tại A

\( \Rightarrow \)AO vừa là phân giác \(\angle BAC\)  vừa là đường trung trực của BC (tính chất tam giác cân)

c) Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với \(\left( O \right)\) (E không trùng với D). Chứng minh \(\dfrac{{DE}}{{BE}} = \dfrac{{BD}}{{BA}}\).

Ta có D đối xứng với B qua O\( \Rightarrow \)BD là đường kính của \(\left( O \right)\)

\( \Rightarrow \)\(\angle BED = {90^o}\) (góc nội tiếp chắn nửa đường tròn)

Xét \(\Delta BED\) và \(\Delta ABD\) có: \(\angle BED = \angle ABD = {90^o}\), \(\angle D\) chung

d) Tính số đo góc HEC.

\(\angle BCD = {90^o}\) (góc nội tiếp chắn nửa đường tròn)

\(\angle AHB = {90^o}\) (AO là trung trực của BC)

Xét \(\Delta BCD\) và \(\Delta AHB\) có: \(\angle BCD = \angle AHB = {90^o},\;\angle BDC = \angle ABH\)(BA là tiếp tuyến của \(\left( O \right)\) tại B)

   kết hợp c) \( \Rightarrow \dfrac{{DE}}{{BE}} = \dfrac{{CD}}{{BH}}\)

Xét \(\Delta BHE\) và \(\Delta DCE\) có     (2 góc t.ư)

\( \Rightarrow \angle BEH + \angle HED = \angle DEC + \angle HED \Rightarrow \angle BED = \angle HEC\)

Mà \(\angle BED = {90^o}\) (chứng minh trên)

Vậy \(\angle HEC = {90^o}\)

LG bài 5

Lời giải chi tiết:

Cho \(x > 0,\,\,y > 0\) thỏa mãn \(xy = 6\). Tìm giá trị nhỏ nhất của biểu thức:

\(Q = \dfrac{2}{x} + \dfrac{3}{y} + \dfrac{6}{{3x + 2y}}\) .

\(Q = \dfrac{2}{x} + \dfrac{3}{y} + \dfrac{6}{{3x + 2y}} = \dfrac{{2y + 3x}}{{xy}} + \dfrac{6}{{3x + 2y}} = \dfrac{{3x + 2y}}{6} + \dfrac{6}{{3x + 2y}}\)

Đặt \(t = 3x + 2y \Rightarrow t \ge 2\sqrt {3x.2y}  \Leftrightarrow t \ge 2\sqrt {6.6}  = 12\)

Theo bất đẳng thức AM-GM và vì \(t \ge 12\) nên ta có:

\(Q = \dfrac{t}{6} + \dfrac{6}{t} = \left( {\dfrac{t}{6} + \dfrac{{24}}{t}} \right) - \dfrac{{18}}{t} \ge 2\sqrt {\dfrac{t}{6}.\dfrac{{24}}{t}}  - \dfrac{{18}}{{12}} = \dfrac{5}{2}\)

Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}3x = 2y\\xy = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{2y}}{3}\\\dfrac{{2{y^2}}}{3} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{2y}}{3}\\{y^2} = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\;\;\left( {do\;\;y > 0} \right)\end{array} \right.\)

Vậy giá trị nhỏ nhất của Q là \(\dfrac{5}{2}\) đạt được khi \(\left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\).

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 9 tại Tuyensinh247.com

Loigiaihay.com