Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 6. Tính chất của hai tiếp tuyến cắt nhau

Đề kiểm tra 15 phút - Đề số 6 - Bài 6 - Chương 2 - Hình học 9


Giải Đề kiểm tra 15 phút - Đề số 6 - Bài 6 - Chương 2 - Hình học 9

Đề bài

Từ điểm P nằm ngoài đường tròn (O; R), vẽ hai tiếp tuyến PA, PB (A, B là các tiếp điểm). Gọi H là chân đường vuông góc kẻ từ A đến đường kính BC. Chứng minh rằng PC cắt AH tại trung điểm I của AH.

Phương pháp giải - Xem chi tiết

Sử dụng:

+Tính chất hai tiếp tuyến cắt nhau

 

+Định lý talet trong tam giác

Lời giải chi tiết

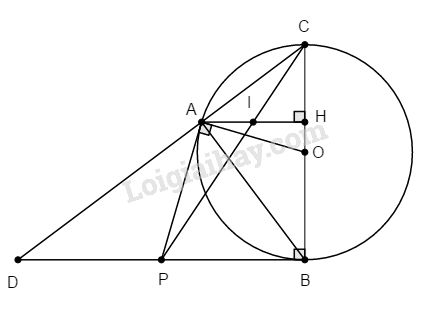
Gọi D là giao điểm của đường thẳng AC và BP.

Ta có: \(\widehat {BAC} = 90^\circ \) (BC là đường kính)

\( \Rightarrow \widehat {BAD} = 90^\circ \) (kề bù) hay \(\widehat {DAP} + \widehat {PAB} = 90^\circ \) (1)

∆ABD vuông tại A (cmt) \( \Rightarrow \widehat {ABD} + \widehat {ADB} = 90^\circ \) (2)

Mặt khác PA, PB là hai tiếp tuyến cuả (O)

nên \(PA = PB\) và \(\widehat {PAB} = \widehat {PBA}\) (3)

Từ (1), (2) và (3) \( \Rightarrow \widehat {DAP} = \widehat {ADP}\)

Do đó ∆APD cân tại P

\(⇒ PA = PD\), mà \(PA = PB\) (tính chất hai tiếp tuyến cắt nhau)

\(⇒ PD = PB.\)

Lại có DB // AH (⊥ BC)

Xét ∆PBC có : IH // PB \( \Rightarrow {{IH} \over {PB}} = {{IC} \over {PC}}\) (4) (Định lí Ta-lét)

Tương tự ∆PCD có : AI // PD \( \Rightarrow {{AI} \over {DP}} = {{IC} \over {PC}}\) (5)

Từ (4) và (5) \( \Rightarrow {{IH} \over {PB}} = {{AI} \over {DP}} \Rightarrow IH = IA\) (vì \(PB = PD\))

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store