 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 6. Tính chất của hai tiếp tuyến cắt nhau
Bài 6. Tính chất của hai tiếp tuyến cắt nhau
Bài 26 trang 115 SGK Toán 9 tập 1
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn.
Đề bài
Cho đường tròn \((O)\), điểm \(A\) nằm bên ngoài đường tròn. Kẻ các tiếp tuyến \(AB,\ AC\) với đường tròn (\(B,\ C\) là các tiếp điểm).
a) Chứng minh rằng \(OA\) vuông góc với \(BC\).
b) Vẽ đường kính \(CD\). Chứng minh rằng \(BD\) song song với \(AO\).
c) Tính độ dài các cạnh của tam giác \(ABC\); biết \(OB=2cm,\ OA=4cm\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Tính chất hai tiếp tuyến cắt nhau: cho \((O;R)\) với hai tiếp tuyến \(AB,\ AC\). Khi đó:
+) \(AB=AC\)
+) \(AO\) là phân giác của góc \(BAC\)
b) Sử dụng tính chất: nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác thì tam giác đó là tam giác vuông (Bài tập 3 - trang 100)
c) +) Dùng định nghĩa tỉ số lượng giác trong tam giác vuông: \(\sin \alpha = \dfrac{cạnh\ đối}{cạnh\ huyền}\) để tính số đo góc.
+) Tam giác cân có một góc bằng \(60^o\) thì là tam giác đều.
+) Dùng định lí Pytago: \(\Delta{ABC}\) vuông tại \(A\) thì \(BC^2=AC^2+AB^2\).
Lời giải chi tiết
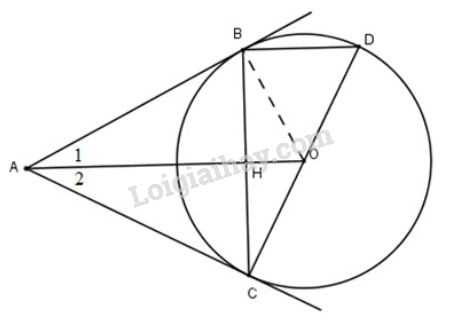
a) Vì \(AB,\ AC\) là các tiếp tuyến cắt nhau tại A nên \(AB=AC\) và \(\widehat{A_{1}}=\widehat{A_{2}}\) (tính chất hai tiếp tuyến cắt nhau)
Suy ra \(\Delta{ABC}\) cân tại \(A\).
Vì \(\widehat{A_{1}}=\widehat{A_{2}}\) nên \(AO\) là tia phân giác của góc \(A\) nên \(AO\) đồng thời là đường cao ứng với cạnh \(BC\).
Vậy \(OA\perp BC\)
b) Điểm \(B\) nằm trên đường tròn đường kính \(CD\) nên \(\widehat{CBD}=90^{\circ}\) (bài 3 trang 100 SGK toán 9 tập 1) hay \(BC \bot BD\).
Lại có \(AO \bot BC\)
Suy ra \(BD // AO\) (vì cùng vuông góc với \(BC)\).
c) Nối \(OB\) thì \(OB \perp AB.\)
Xét tam giác \(AOB\) vuông tại \(B\), ta có:
\(\sin \widehat {{A_1}} = \dfrac{OB}{OA}=\dfrac{2}{4}=\dfrac{1}{2}\)
\(\Rightarrow \widehat{A_{1}}=30^{\circ}\)\(\Rightarrow \widehat{BAC}=2.\widehat {A_1}=60^{\circ}.\)
Tam giác \(ABC\) cân, có một góc \(60^{\circ}\) nên là tam giác đều.
Suy ra \(AB=BC=CA\)
Xét tam giác \(AOB\) vuông tại \(B\), áp dụng định lí Pytago, ta có:
\(AO^{2}=AB^{2}+OB^{2} \Rightarrow AB^2=AO^2-OB^2\)
\(\Leftrightarrow AB^2=4^{2}-2^{2}=16-4=12 \Rightarrow AB=2\sqrt{3.}\)
Vậy \(AB=AC=BC=2\sqrt{3}cm\).
Nhận xét. Qua câu c) ta thấy: Góc tạo bởi hai tiếp tuyến của một đường tròn vẽ từ một điểm cách tâm một khoảng bằng đường kính đúng bằng \(60^{\circ}\).
Cách khác câu b:
Gọi H là giao điểm của OA và BC.
Vì \(OA \bot BC\) tại H mà OA là 1 phần đường kính và BC là dây của đường tròn (O) nên H là trung điểm của BC (định lý)
Lại có O là trung điểm của đường kính CD nên OH là đường trung bình của tam giác BCD
Hay OH//BD. Do đó, OA//BD.
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận