 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 6. Tính chất của hai tiếp tuyến cắt nhau
Bài 6. Tính chất của hai tiếp tuyến cắt nhau
Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 2 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 2 - Hình học 9
Đề bài
Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc (O), tiếp tuyến A của (O) cắt BC tại D. Gọi M là trung điểm của AD.
a. Chứng minh MC là tiếp tuyến của (O).
b. Chứng minh \(MO ⊥ AC\) tại trung điểm I của AC.
Phương pháp giải - Xem chi tiết
a.Sử dụng:
+Góc nội tiếp chắn nửa đường tròn bằng 90 độ
+Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền
b. Sử dụng
+Tính chất hai tiếp tuyến cắt nhau
+Đường trung trực của đoạn thẳng
Lời giải chi tiết
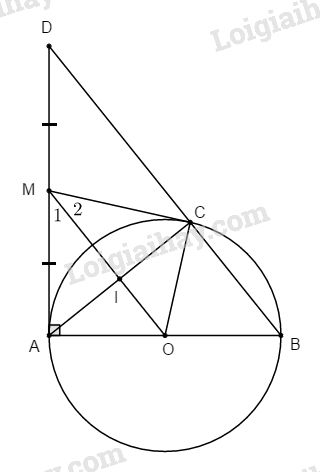
a. Ta có: \(\widehat {ACB} = 90^\circ \) (chắn nửa đường tròn)
\( \Rightarrow \widehat {ACD} = 90^\circ \) (kề bù)
∆ACD vuông có CM là đường trung tuyến
\( \Rightarrow CM = MA = {{AD} \over 2}\)
Do đó hai tam giác vuông MCO và MAO bằng nhau (c.c.c)
\( \Rightarrow \widehat {MCO} = \widehat {MAO} = 90^\circ \) hay MC là tiếp tuyến của (O)
b. Ta có: \(MA = MC\) (tính chất hai tiếp tuyến cắt nhau)
\(OA = OC (=R)\)
\(⇒ OM\) là đường trung trực của đoạn AC hay \(OM ⊥ AC.\)
Loigiaihay.com
- Đề kiểm tra 15 phút - Đề số 5 - Bài 6 - Chương 2 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 6 - Bài 6 - Chương 2 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 7 - Bài 6 - Chương 2 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 8 - Bài 6 - Chương 2 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 9 - Bài 6 - Chương 2 - Hình học 9
>> Xem thêm
Các bài khác cùng chuyên mục












Danh sách bình luận