-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
-
Chủ đề 1 : Phép nhân đa thức – Hằng đẳng thức đáng nhớ
-
Chủ đề 2 : Phân tích đa thức thành nhân tử
- 1. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- 2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- 3. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- 4. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
- Luyện tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
-
Chủ đề 3: Phép chia đa thức
-
Ôn tập chương 1 - Phép nhân và phép chia đa thức
-
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
-
CHƯƠNG 1. TỨ GIÁC
-
Chủ đề 1 : Tứ giác – Hình thang
-
Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- 1. Đối xứng trục
- 2. Hình bình hành
- 3. Đối xứng tâm
- 4. Hình chữ nhật
- 5. Tập hợp các điểm cách đều một đường thẳng cho trước
- 6. Hình thoi
- 7. Hình vuông
- Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
-
Ôn tập chương 1 - Tứ giác
-
-
CHƯƠNG 2. ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
-
CHƯƠNG 3 : PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN – GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
-
CHƯƠNG 4. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
CHƯƠNG 3. TAM GIÁC ĐỒNG DẠNG
-
Chủ đề 1 : Định lí Thales
-
Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- 1. Khái niệm hai tam giác đồng dạng
- 2. Trường hợp đồng dạng thứ nhất (c.c.c)
- 3. Trường hợp đồng dạng thứ hai (c.g.c)
- 4. Trường hợp đồng dạng thứ ba (g.g)
- 5. Các trường hợp đồng dạng của tam giác vuông
- 6. Ứng dụng thực tế của tam giác đồng dạng
- Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
-
-
CHƯƠNG 4 : HÌNH LĂNG TRỤ ĐỨNG – HÌNH CHÓP ĐỀU
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – H..
Bài tập 6 trang 133 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cần thêm điều kiện gì để các tứ giác ở hình dưới đây trở thành hình bình hành:
Đề bài
Cần thêm điều kiện gì để các tứ giác ở hình dưới đây trở thành hình bình hành:
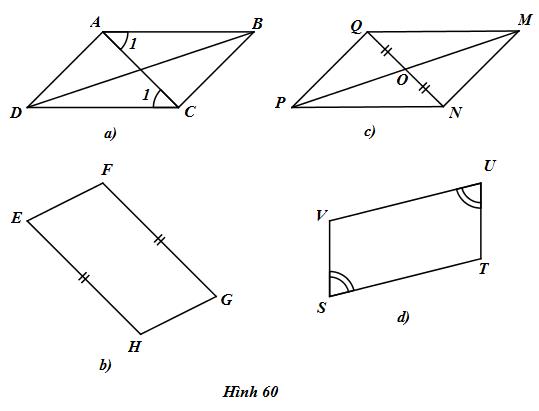
Lời giải chi tiết
a) Ta có: \(\widehat {BAC} = \widehat {ACD}\,\,\left( {gt} \right)\) mà \(\widehat {BAC}\) và \(\widehat {ACD}\) ở vị trí so le trong nên AB // CD.
Cần thêm điều kiện \(AB = CD\) để ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành)
b) Ta có \(EH = GH\,\,\left( {gt} \right)\)
Cần thêm điều kiện \(EF = HG\) để EFGH là hình bình hành (dấu hiệu nhận biết hình bình hành)
c) O là trung điểm của QN \(\left( {OQ = ON} \right)\)
Cần O là trung điểm của PM để MNPQ là hình bình hành (dấu hiệu nhận biết hình bình hành)
d) \(\widehat S = \widehat U\)
Cần thêm điều kiện \(\widehat V = \widehat T\) để VUTS là hình bình hành (dấu hiệu nhận biết hình bình hành).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài tập 7 trang 134 Tài liệu dạy – học Toán 8 tập 1
- Bài tập 8 trang 134 Tài liệu dạy – học Toán 8 tập 1
- Bài tập 9 trang 134 Tài liệu dạy – học Toán 8 tập 1
- Bài tập 10 trang 134 Tài liệu dạy – học Toán 8 tập 1
- Bài tập 11 trang 134 Tài liệu dạy – học Toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
