 Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
 Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – H..
Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – H..
Bài tập 30 trang 137 Tài liệu dạy – học Toán 8 tập 1
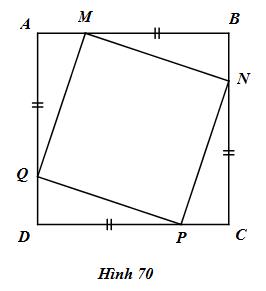
Giải bài tập Ở hình 70, cho biết ABCD là một hình vuông. Lấy các điểm M, N, P, Q lần lượt trên AB, BC, CD, DA sao cho MB = NC = PD = QA. Chứng minh rằng tứ giác MNPQ là hình vuông.
Đề bài
Ở hình 70, cho biết ABCD là một hình vuông. Lấy các điểm M, N, P, Q lần lượt trên AB, BC, CD, DA sao cho \(MB = NC = PD = QA.\) Chứng minh rằng tứ giác MNPQ là hình vuông.
Lời giải chi tiết
Ta có:
\(AB = BC = CD = AD\) (ABCD là hình vuông)
\(\eqalign{ & MB = NC = DP = AQ\,\,\left( {gt} \right) \cr & \Rightarrow AM = BN = CP = DQ \cr} \)
Xét \(\Delta MBN\) và \(\Delta NPC\) có :
\(MB = NC\,\,\left( {gt} \right)\)
\(BN = PC\,\,\left( {cmt} \right)\)
\(\widehat {MBN} = \widehat {NCP}\,\,\left( { = {{90}^0}} \right)\)
\( \Rightarrow \Delta MBN = \Delta NCP\,\,\left( {c.g.c} \right) \Rightarrow MN = NP\) và \(\widehat {MNB} = \widehat {NPC}\)
Chứng minh tương tự ta có : \(\Delta QAM = \Delta PDQ;\,\,\Delta MBN = \Delta QAM\)
\( \Rightarrow QM = PQ,\,\,MN = QM \Rightarrow MN = NP = QM = PQ\).
Do đó tứ giác MNPQ là hình thoi.
Mặt khác \(\widehat {MNB} + \widehat {CNP} = \widehat {NPC} + \widehat {CNP} = {90^0} \Rightarrow \widehat {MNP} = {90^0}\)
Hình thoi MNPQ có \(\widehat {MNP} = {90^0}\) nên là hình vuông.
Loigiaihay.com












Danh sách bình luận