Bài 59 trang 92 SGK Toán 8 tập 2

Hình thang ABCD (AB//CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD.

Đề bài

Hình thang \(ABCD \,(AB//CD)\) có \(AC\) và \(BD\) cắt nhau tại \(O, AD\) và \(BC\) cắt nhau tại \(K\). Chứng minh rằng \(OK\) đi qua trung điểm của các cạnh \(AB\) và \(CD\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Qua \(O\) kẻ đường thẳng song song với \(AB, CD\) cắt \(AD, BC\) lần lượt tại \(E, F\).

- Chứng minh \(\dfrac{{AN}}{{EO}}=\dfrac{{BN}}{{FO}}\).

- Chứng minh \(\dfrac{{EO}}{{DM}}=\dfrac{{FO}}{{CM}}\).

Lời giải chi tiết

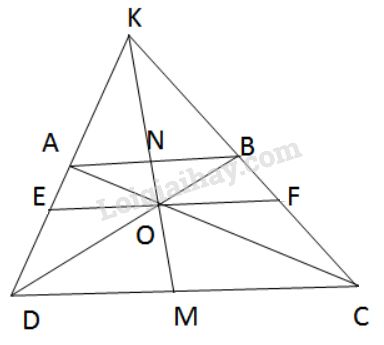
Qua \(O\) kẻ đường thẳng song song với \(AB, CD\) cắt \(AD, BC\) lần lượt tại \(E, F\).

Suy ra \(AB//EF//CD\)

Gọi N là giao của KO và AB, M là giao của KO với DC.

Ta có: \(OE // DC\) (gt)

\( \Rightarrow \dfrac{{OE}}{{DC}} = \dfrac{{AO}}{{AC}}\left( 1 \right)\) (hệ quả của định lí TaLet)

\(OF // DC\) (gt)

\( \Rightarrow \dfrac{{OF}}{{DC}} = \dfrac{{BF}}{{BC}}\left( 2 \right)\) (hệ quả của định lí TaLet)

\(OF // AB\) (gt)

\( \Rightarrow \dfrac{{BF}}{{BC}} = \dfrac{{OA}}{{AC}}\) (3) (hệ quả của định lí TaLet)

Từ (1), (2) và (3) ta có:

\(\dfrac{{OE}}{{DC}} = \dfrac{{OF}}{{DC}} \Rightarrow OE = OF\)

Ta có: \(AB//EF\) (gt) áp dụng hệ quả của định lí TaLet ta có:

\(\begin{array}{l}
\Rightarrow \dfrac{{AN}}{{EO}} = \dfrac{{KN}}{{K{\rm{O}}}};\,\dfrac{{BN}}{{F{\rm{O}}}} = \dfrac{{KN}}{{K{\rm{O}}}}\\
\Rightarrow \dfrac{{AN}}{{EO}} = \dfrac{{BN}}{{F{\rm{O}}}} \\\text{Mà } EO=FO\\ \Rightarrow AN = BN
\end{array}\)

\( \Rightarrow \) \(N\) là trung điểm của \(AB.\)

Tương tự ta có: \(EF // DC\) (gt) áp dụng hệ quả của định lí TaLet ta có:

\(\begin{array}{l}
\Rightarrow \dfrac{{EO}}{{DM}} = \dfrac{{KO}}{{K{\rm{M}}}};\,\dfrac{{FO}}{{C{\rm{M}}}} = \dfrac{{KO}}{{K{\rm{M}}}}\\
\Rightarrow \dfrac{{EO}}{{DM}} = \dfrac{{FO}}{{C{\rm{M}}}}\\\text{Mà }EO=FO\\ \Rightarrow DM = CM
\end{array}\)

\( \Rightarrow M\) là trung điểm của \(CD\).

Vậy \(OK\) đi qua trung điểm của các cạnh \(AB\) và \(CD\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 89 phiếu

Bài tiếp theo

Bài 60 trang 92 SGK Toán 8 tập 2
Cho tam giác vuông ABC, và đường phân giác BD (D thuộc cạnh AC).
Bài 61 trang 92 SGK Toán 8 tập 2
Giải bài 61 trang 92 SGK Toán 8 tập 2. Tứ giác ABCD có AB = 4cm, BC = 20 cm, CD = 25 cm, DA = 8cm, đường chéo BD = 10cm.
Lý thuyết Ôn tập chương 3. Tam giác đồng dạng
Lý thuyết Ôn tập chương 3. Tam giác đồng dạng
Bài 58 trang 92 SGK Toán 8 tập 2
Giải bài 58 trang 92 SGK Toán 8 tập 2. Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (H.66
Bài 57 trang 92 SGK Toán 8 tập 2
Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M.
Bài 56 trang 92 SGK Toán 8 tập 2
Giải bài 56 trang 92 SGK Toán 8 tập 2. Xác định tỉ số của hai đoạn thẳng AB và CD trong các trường hợp sau: