Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Ôn tập chương III: Tam giác đồng dạng

Bài 57 trang 92 SGK Toán 8 tập 2


Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M.

Đề bài

Cho tam giác \(ABC (AB < AC)\). Vẽ đường cao \(AH\), đường phân giác \(AD\), đường trung tuyến \(AM\). Có nhận xét gì về vị trí của ba điểm \(H, D, M\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Áp dụng: Tính chất đường phân giác của tam giác, quan hệ giữa cạnh và góc trong tam giác.

Lời giải chi tiết

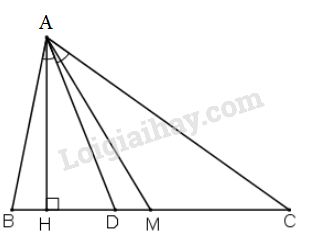
+ Nhận xét: \(D\) luôn nằm giữa \(H\) và \(M\).

+ Chứng minh:

\(AD\) là đường phân giác của \(∆ABC\).

\(\Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{DB}}{{DC}}\) (tính chất đường phân giác của tam giác)

Mà \(AB < AC\) (giả thiết)

\( \Rightarrow DB < DC\) \( \Rightarrow  DB + DC < DC + DC\)

\( \Rightarrow BD + DC < 2DC\) hay \(BC < 2DC\) 

\( \Rightarrow  DC >\dfrac{{BC}}{2}\)

Mà \(MC = \dfrac{{BC}}{2}\) (\(M\) là trung điểm của \(BC\))

\( \Rightarrow DC > MC\) \( \Rightarrow M \) nằm giữa \(D\) và \(C\) (1)

+ Mặt khác: \(\widehat {CAH} = {90^0} - \hat C\) (\(∆CAH\) vuông tại \(H\))

\(\hat A + \hat B + \hat C = {180^0}\) (tổng 3 góc ∆ABC)

\( \Rightarrow \widehat {CAH} = \dfrac{{\widehat A + \widehat B + \widehat C}}{2} - \widehat C\)

\( \Rightarrow \widehat {CAH} = \dfrac{{\widehat A}}{2} + \dfrac{{\widehat B}}{2} - \dfrac{{\widehat C}}{2}\)\(\, = \dfrac{{\widehat A}}{2} + \dfrac{{\widehat B - \widehat C}}{2}\)

Vì \(AB < AC\) \( \Rightarrow \widehat C < \widehat B\) ( quan hệ giữa cạnh và góc đối diện trong tam giác)

\(\Rightarrow \frac{\widehat B - \widehat C}{2} > 0\)

Do đó: \(\widehat {CAH} >  \dfrac{{\widehat A}}{2}\) hay \(\widehat {CAH} > \widehat {CAD}\)

\( \Rightarrow \) Tia \(AD\) nằm giữa hai tia \(AH\) và \(AC\)

Do đó \(D\) nằm giữa hai điểm \(H\) và \(C\) (2)

Từ (1) và (2) suy ra \(D\) nằm giữa \(H\) và \(M.\)

Loigiaihay.com


Bình chọn:
4.6 trên 84 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua