Bài 4 trang 7 SGK Toán 8 tập 2
Nối mỗi phương trình sau với các nghiệm của nó:
Đề bài
Nối mỗi phương trình sau với các nghiệm của nó:
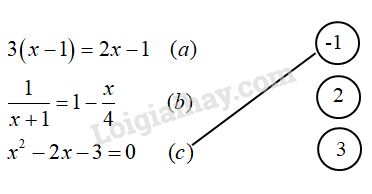
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Thay các giá trị của \(x=-1\), \(x=2\) và \(x=3\) vào từng phương trình (a), (b), (c); giá trị nào thỏa mãn phương trình thì là nghiệm của phương trình đó.
Lời giải chi tiết
*) Xét phương trình \(3(x-1)=2x-1\;\;\;\;\;(1)\)
+) Thay \(x=-1\) vào vế trái và vế phải của phương trình (1) ta được:
\(\eqalign{
& VT = 3.\left( { - 1 - 1} \right) = 3.\left( { - 2} \right) = - 6 \cr
& VP = 2.\left( { - 1} \right) - 1 = - 2 - 1 = - 3 \cr} \)
\( - 6 \ne - 3 \Rightarrow VT \ne VP\)
Vậy \(x=-1\) không là nghiệm của phương trình (1)
+) Thay \(x=2\) vào vế trái và vế phải của phương trình (1) ta được:
\(\eqalign{
& VT = 3.\left( {2 - 1} \right) = 3.1 = 3 \cr
& VP = 2.2 - 1 = 4 - 1 = 3 \cr} \)
\(3 = 3 \Rightarrow VT = VP\)
Vậy \(x=2\) là nghiệm của phương trình (1)
+) Thay \(x=3\) vào vế trái và vế phải của phương trình (1) ta được:
\(\eqalign{
& VT = 3.\left( {3 - 1} \right) = 3.2 = 6 \cr
& VP = 2.3 - 1 = 6 - 1 = 5 \cr} \)
\(6 \ne 5 \Rightarrow VT \ne VP\)
Vậy \(x=3\) không là nghiệm của phương trình (1)
*) Xét phương trình \(\dfrac{1}{{x + 1}} = 1 - \dfrac{x}{4}\;\;\;\;\;(2)\)
+) Với \(x=-1\) thì phương trình (2) không xác định nên \(x=-1\) không là nghiệm của phương trình (2)
+) Thay \(x=2\) vào vế trái và vế phải của phương trình (2) ta được:
\(\eqalign{
& VT = {1 \over {2 + 1}} = {1 \over 3} \cr
& VP = 1 - {2 \over 4} = 1 - {1 \over 2} = {1 \over 2} \cr} \)
\(\dfrac{1}{3} \ne \dfrac{1}{2} \Rightarrow VT \ne VP\)
Vậy \(x=2\) không là nghiệm của phương trình (2)
+) Thay \(x=3\) vào vế trái và vế phải của phương trình (2) ta được:
\(\eqalign{
& VT = {1 \over {3 + 1}} = {1 \over 4} \cr
& VP = 1 - {3 \over 4} = {4 \over 4} - {3 \over 4} = {1 \over 4} \cr} \)
\(\dfrac{1}{4} = \dfrac{1}{4} \Rightarrow VT = VP\)
Vậy \(x=3\) là nghiệm của phương trình (2)
*) Xét phương trình \({x^2} - 2x - 3 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,(3)\)
+) Thay \(x=-1\) vào vế trái và vế phải của phương trình (3) ta được:
\(\eqalign{
& VT = {\left( { - 1} \right)^2} - 2.\left( { - 1} \right) - 3\cr&\;\;\;\;\;\;\; = 1 + 2 - 3 = 0 \cr
& VP = 0 \cr} \)
\(0 = 0 \Rightarrow VT = VP\)
Vậy \(x=-1\) là nghiệm của phương trình (3)
+) Thay \(x=2\) vào vế trái và vế phải của phương trình (3) ta được:
\(\eqalign{
& VT = {2^2} - 2.2 - 3 = 4 - 4 - 3 = - 3 \cr
& VP = 0 \cr} \)
\( - 3 \ne 0 \Rightarrow VT \ne VP\)
Vậy \(x=2\) không là nghiệm của phương trình (3)
+) Thay \(x=3\) vào vế trái và vế phải của phương trình (3) ta được:
\(\eqalign{
& VT = {3^2} - 2.3 - 3 = 9 - 6 - 3 = 0 \cr
& VP = 0 \cr} \)
\(0 = 0 \Rightarrow VT = VP\)
Vậy \(x=3\) là nghiệm của phương trình (3)
Ta nối như sau:

Loigiaihay.com













Danh sách bình luận