 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Ôn tập chương III – Góc với đường tròn
Ôn tập chương III – Góc với đường tròn
Đề kiểm tra 45 phút (1 tiết) - Đề số 6 - Chương 3 - Hình học 9
Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 6 - Chương 3 - Hình học 9
Đề bài
Bài 1: Cho đường tròn (O; R) dây \(AB = R\sqrt 2 \). Từ A và B vẽ hai tiếp tuyến cắt nhau tại C. Đường thẳng OC cắt cung nhỏ AB tại I. Chứng minh rằng I là tâm đường tròn nội tiếp ∆ABC.
Bài 2: Cho hình bình hành ABCD (\(\widehat A > 90^\circ \)). Đường tròn tâm O ngoại tiếp tam giác ABC cắt DC tại M và cắt BD tại N.
a) Chứng tỏ: AM = AD.
b) Tính độ dài cung nhỏ MB theo R nếu góc ADC bằng 60º và OA = R
c) Gọi I là giao điểm của AC và BD. Chứng tỏ : IA2 = IN.IB.
d) Chứng tỏ IA là tiếp tuyến của đường tròn ngoại tiếp ∆AND.
LG bài 1
+ Tứ giác có ba góc vuông là hình chữ nhật
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
+ Góc giữa tiếp tuyến và dây bằng nửa số đo cung bị chắn
+ Góc nội tiếp bằng nửa số đo cung bị chắn
Lời giải chi tiết:
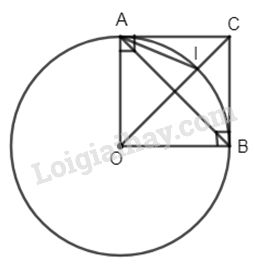
Ta có : \(AB = R\sqrt 2 \Rightarrow \widehat {AOB} = 90^\circ \)
Dễ thấy tứ giác ACBO là hình chữ nhật ( ba góc vuông).
Lại có \(OA = OB ( = R)\) nên ACBO là hình vuông \( \Rightarrow \) OC là tia phân giác của \(\widehat {ACB}\).
Mặt khác \(\widehat {CAI} = \dfrac{1}{2}\overparen{AI}\) ( góc giữa tiếp tuyến và một dây)
\(\widehat {IAB} = \dfrac{1}{2}\overparen{BI}\) ( góc nội tiếp)
mà \(\overparen{ AI} = \overparen{ BI}\) \( \Rightarrow \widehat {CAI} = \widehat {IAB}\) hay AI là tia phân giác của \(\widehat {CAB}\).
Do đó I là tâm đường tròn nội tiếp ∆ABC.
LG bài 2
Phương pháp giải:
Sử dụng:
+Tính chất của tứ giác nội tiếp
+Tính chất hình bình hành
+Tính chất tam giác cân
+Công thức: \(l = \frac{{\pi Rn}}{{180}}\)
+Tam giác đồng dạng
Lời giải chi tiết:
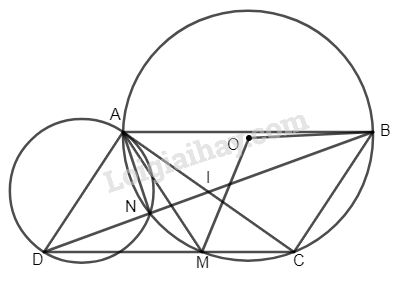
a) Ta có tứ giác ABCM nội tiếp
\( \Rightarrow \widehat {AMD} = \widehat {ABC}\) (cùng bù với \(\widehat {AMC}\))
mà \(\widehat {ABC} = \widehat {ADC}\) ( góc đối của hình bình hành)
\( \Rightarrow \widehat {AMD} = \widehat {ADC}\)
Do đó ∆ADM cân tại A
\( \Rightarrow AM = AD.\)
b) Khi \(\widehat {ADC} = 60^\circ \)
\( \Rightarrow \widehat {DAB} = 180^\circ - 60^\circ = 120^\circ \)
Mặt khác ∆ADM cân có
\(\widehat {ADC} = 60^\circ \) nên ∆ADM đều \( \Rightarrow \widehat {DAM} = 60^\circ \)
Do đó \(\widehat {MAB} = 60^\circ \Rightarrow \widehat {MOB} = 120^\circ \) ( góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung)
Vậy \({l_{\overparen{MB}}} =\dfrac {{\pi R.120} }{ {180}} =\dfrac {{2\pi R} }{ 3}\).
c) Xét ∆AIN và ∆BIC có
+) \(\widehat {AIN} = \widehat {BIC}\) ( đối đỉnh)
+) \(\widehat {NAI} = \widehat {NBC}\) ( góc nội tiếp chắn cung NC)
Do đó ∆AIN và ∆BIC đồng dạng (g.g)
\( \Rightarrow \dfrac{{IA} }{{IB}} = \dfrac{{IN} }{ {IC}} \Rightarrow IA.IC = IN.IB\)
(mà IC = IA) \(\Rightarrow IA^2= IN.IB.\)
d) Gọi IA’ là tiếp tuyến của đường tròn ngoại tiếp ∆AND, ta dễ dàng chứng minh được IA2 = IN.IB mà IA2 = IN.IB (cmt)
\( \Rightarrow IA{^2} = I{A^2} \Rightarrow IA = IA\) hay A’ trùng với A.
Vậy IA là tiếp tuyến của đường tròn ngoại tiếp ∆AND.
Loigiaihay.com
- Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 3 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 3 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 3 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 3 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương 3 - Hình học 9
>> Xem thêm
Các bài khác cùng chuyên mục












Danh sách bình luận