 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Ôn tập chương III – Góc với đường tròn
Ôn tập chương III – Góc với đường tròn
Bài 91 trang 104 SGK Toán 9 tập 2
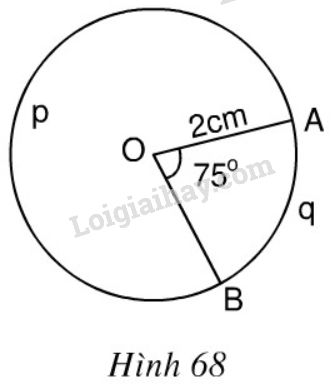
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75^0.
Đề bài
Trong hình 68, đường tròn tâm O có bán kính \(R = 2cm\), góc \(AOB = 75^0\).
a) Tính số đo cung \(ApB\).
b) Tính độ dài hai cung \(AqB\) và \(ApB\).
c) Tính diện tích hình quạt tròn \(OAqB\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Trên đường tròn bán kính R, độ dài l của 1 cung \({n^0}\) được tính theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\)
+) Diện tích hình quạt tròn bán kính R, cung \({n^0}\) được tính theo công thức: \(S = \dfrac{{\pi {R^2}n}}{{360}}\left( {hay\,\,S = \dfrac{{lR}}{2}} \right)\)
Lời giải chi tiết
a) Ta có \(\widehat {AOB}\) là góc ở tâm chắn cung \(AqB\) nên:
\(\widehat {AOB}\) = \(sđ\overparen{AqB}\) hay \(sđ\overparen{AqB}=75^0\)
Vậy \(sđ\overparen{ApB}\) \(=360°- \overparen{AqB}\) \(=360^0 - 75^0 = 285^0\)
b) \({l_{\overparen{AqB}}}\) là độ dài cung \(AqB\), ta có:
\(\displaystyle {l_{\overparen{AqB}}}\) \(=\displaystyle {{\pi Rn} \over {180}} = {{\pi .2.75} \over {180}} = {5 \over 6}\pi (cm)\)
Gọi \({l_{\overparen{ApB}}}\) là độ dài cung \(ApB\) ta có:
\(\displaystyle {l_{\overparen{ApB}}}= {{\pi Rn} \over {180}} = {{\pi .2.285} \over {180}} = {{19\pi } \over 6}(cm)\)
c) Diện tích hình quạt tròn \(OAqB\) là: \(\displaystyle {S_{OAqB}} = {{\pi {R^2}n} \over {360}} = {{\pi {2^2}.75} \over {360}} = {{5\pi } \over 6}(c{m^2})\)
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận