Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Ôn tập chương III – Góc với đường tròn

Bài 97 trang 105 SGK Toán 9 tập 2


Đề bài

Cho tam giác \(ABC\) vuông ở \(A\). Trên \(AC\) lấy một điểm \(M\) và vẽ đường tròn đường kính \(MC\). Kẻ \(BM\) cắt đường tròn tại \(D\). Đường thẳng \(DA\) cắt đường tròn tại \(S\). Chứng minh rằng:

a) \(ABCD\) là một tứ giác nội tiếp;

b) \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{D}}}\) ;

c) \(CA\) là tia phân giác của góc \(SCB\) 

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+ Sử dụng dấu hiệu nhận biết tứ giác nội tiếp: Nếu hai đỉnh kề một cạnh của một tứ giác cùng nhìn cạnh đối diện dưới các góc bằng nhau thì tứ giác đó là tứ giác nội tiếp.

+ Sử dụng: “Hai góc nội tiếp cùng chắn một cung thì bằng nhau” 

Lời giải chi tiết

 

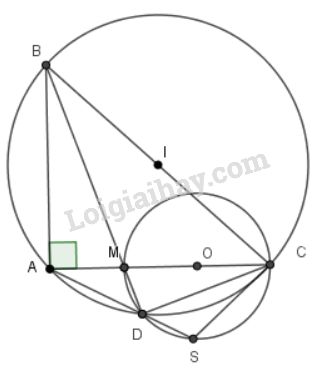
a) Ta có góc \(\widehat {MDC}\) là góc nội tiếp chắn nửa đường tròn \((O)\) nên \(\widehat {MDC} = {90^0}\)

\(\Rightarrow\) \(∆CDB\) là tam giác vuông nên nội tiếp đường tròn đường kính \(BC\).

Ta có \(∆ABC\) vuông tại \(A\).

Do đó \(∆ABC\) nội tiếp trong đường tròn tâm \(I\) đường kính \(BC\).

Ta có \(A\) và \(D\) là hai đỉnh kề nhau cùng nhìn \(BC\) dưới một góc \(90^0\) không đổi nên tứ giác \(ABCD\) nội tiếp đường tròn đường kính \(BC\)

b) Trong đường tròn (I): \(\widehat {AB{\rm{D}}}\)=\(\widehat {AC{\rm{D}}}\) (góc nội tiếp cùng chắn cung \(AD\).

Vậy \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{D}}}\)

c) Ta có:

\(\widehat {ADB} + \widehat {BDS} = {180^0}\) ( 2 góc kề bù)

Mà \(\widehat {MCS} + \widehat {MDS} = {180^0}\) (tứ giác CMDS nội tiếp đường tròn (O))

Từ đó ta có: \(\widehat {ADB}=\widehat {MCS}\) (1)

Lại có tứ giác ABCD nội tiếp nên \(\widehat {ADB}=\widehat {ACB}\)(góc nội tiếp cùng chắn cung AB (2)

Từ (1) và (2) \(\Rightarrow\) \(\widehat {MCS}=\widehat {ACB}\)

Vậy tia \(CA\) là tia phân giác của góc \(SCB\)


Bình chọn:
4 trên 70 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Zalo 2K9 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com, cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua