 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
Đề kiểm tra 15 phút - Đề số 2 - Bài 4 - Chương 1 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 4 - Chương 1 - Hình học 9
Đề bài
Bài 1. Đơn giản biểu thức \(A = \sin \alpha - \sin \alpha .{\cos ^2}\alpha \)
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH và \(BC = a\).
Chứng minh rằng : \(AH = a.{\mathop{\rm sinB}\nolimits} .cosB,\,\)\(BH = a.co{s^2}B,\,CH = a.{\sin ^2}B.\)
Bài 3. Hai cạnh của tam giác là 8cm và 12cm. Góc xen giữa hai cạnh ấy là 30˚. Tính diện tích tam giác.
LG bài 1
Phương pháp giải:
Sử dụng: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Lời giải chi tiết:
Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) (theo câu 1a, đề số 3, §2,3) \( \Rightarrow {\sin ^2}\alpha = 1 - {\cos ^2}\alpha .\)
\(A = \sin \alpha - \sin \alpha .{\cos ^2}\alpha \)
\(\;\;\;\;= \sin \alpha \left( {1 - {{\cos }^2}\alpha } \right)\)
\(\;\;\;\; = \sin \alpha .{\sin ^2}\alpha = {\sin ^3}\alpha \)
LG bài 2
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
a) Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
b) Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.
Lời giải chi tiết:
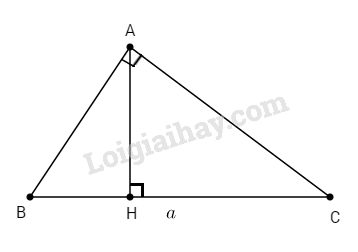
\(∆ABC\) vuông tại A, ta có:
\(AB = AB.{\mathop{\rm cosB}\nolimits} = a.cosB\)
∆AHB vuông tại H, ta có:
\(AH = AB.\sin B = a.\sin B.\cos B\)
Lại có : \(BH = AB.\cos B = a.{\cos ^2}B.\)
Xét tam giác vuông AHC, ta có:
\(CH = AH.\tan \widehat {HAC}\) mà \(\widehat {HAC} = \widehat B\) vì cùng phụ với \(\widehat C\)
Nên \( CH= AH.\tan B\)\(\; = a.\sin B.\cos B.{{\sin B} \over {\cos B}} = a.{\sin ^2}B.\)
LG bài 4
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng
Lời giải chi tiết:
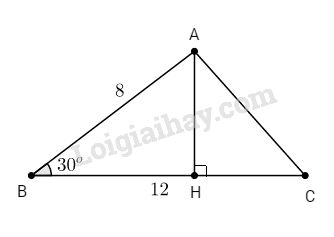
Kẻ đường cao AH của ∆ABC, ta có:
\(AH = AB.\sin B = 8.\sin30^o = 4 (cm)\)
Vậy \({S_{ABC}} = {1 \over 2}.BC.AH = {1 \over 2}.12.4 \)\(\;= 24\,\left( {c{m^2}} \right)\)
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận