Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 30 trang 89 SGK Toán 9 tập 1


Cho tam giác ABC, trong đó BC = 11cm,

Đề bài

Cho tam giác \(ABC\), trong đó \(BC=11cm\), \(\widehat{ABC}=38^{\circ},\widehat{ACB}=30^{\circ}.\) Gọi điểm \(N\) là chân của đường vuông góc kẻ từ \(A\) đến cạnh \(BC\). Hãy tính:

a) Đoạn thẳng \(AN\);

b) Cạnh \(AC\).

Gợi ý: Kẻ \(BK\) vuông góc với \(AC\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+) Tam giác \(ABC\) vuông tại \(A\) thì \(\widehat{B}+\widehat{C}=90^o\).

+) Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác \(ABC\) vuông tại \(A\) thì:

               \(b=a.\sin B \Rightarrow a=\dfrac{b}{\sin B}\); 

              \( b= a . \cos C \Rightarrow a=\dfrac{b}{\cos C}\).                   

Lời giải chi tiết

a) Kẻ \(BK\perp AC\) \((K\in AC)\)

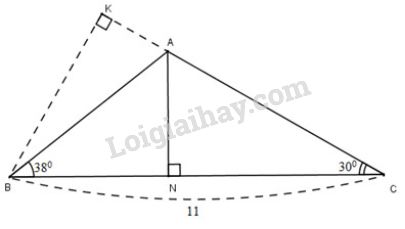
Xét tam giác vuông \(BKC\) ta có: 

 \(\widehat{KBC}+\widehat{KCB}=90^{\circ}\)

\(\Rightarrow \widehat{KBC}=90^o - \widehat{KCB}=90^o -30^{\circ}=60^{\circ}\)

Mà \(\widehat{KBA}+\widehat{ABN}=\widehat{KBN} \Rightarrow \widehat{KBA}=\widehat{KBN}-\widehat{ABN}\)

\(\Leftrightarrow \widehat{KBA}=60^{\circ}-38^{\circ}=22^{\circ}\)

Xét tam giác \(KBC\) vuông tại \(K\) có:

\(BK=BC\cdot \sin C=11\cdot \sin30^{\circ}=5,5(cm)\)

Xét tam giác \(KBA\) vuông tại \(K\) có: 

\(BK=AB. \cos \widehat{KBA} \Leftrightarrow 5,5=AB.\cos 22^o \)

\(\Rightarrow AB=\dfrac{5,5}{\cos 22^{\circ}}\approx 5,932 (cm).\)

Xét tam giác \(ABN\) vuông tại \(N\) có:

\(AN= AB. \sin \widehat{ABN} \approx 5,932.\sin 38^o \approx 3,652(cm)\)

b) Xét tam giác \(ANC\) vuông tại \(N\) có:

\(AN=AC. \sin C \Rightarrow 3,652 = \sin 30^o . AC\)

\(\Leftrightarrow AC=\dfrac{3,652}{\sin 30^o} \approx 7,304(cm)\).

Loigiaihay.com


Bình chọn:
4.7 trên 267 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store