Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 3: Tứ giác nội tiếp

Bài 8 trang 102 Tài liệu dạy – học Toán 9 tập 2


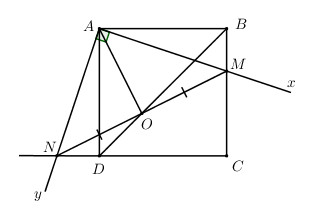
Giải bài tập Cho hình vuông ABCD cạnh bằng a. Góc vuông xAy thay đổi sao cho tia Ax cắt đoạn BC tại M và tia Ay cắt đoạn CD kéo dài tại N.

Đề bài

Cho hình vuông ABCD cạnh bằng a. Góc vuông xAy thay đổi sao cho tia Ax cắt đoạn BC tại M và tia Ay cắt đoạn CD kéo dài tại N.

a) Chứng minh hai tam giác ABM và AND bằng nhau.

b) Gọi O là trung điểm của MN. Chứng minh ABMO và ANDO là các tứ giác nội tiếp.

c) Chứng minh ba điểm B, D, O thẳng hàng.

Phương pháp giải - Xem chi tiết

a) Chứng minh \(\widehat {BAM} = \widehat {DAN}\), chứng minh \({\Delta _v}ABM\) và \({\Delta _v}ADN\) bằng nhau theo trường hợp cạnh góc vuông – góc nhọn.

b) Chứng minh tam giác AMN cân tại A \( \Rightarrow AO \bot MN\).

Chứng minh tứ giác ABMO có tổng hai góc đối bằng 1800.

Chứng minh tứ giác ANDO có hai đỉnh O; D cùng nhìn AN dưới góc 900.

c) Chứng minh hai góc ở vị trí đối đỉnh \(\widehat {BOM}\) và \(\widehat {DON}\) bằng nhau.

Lời giải chi tiết

 

a) Ta có: \(\widehat {BAM} = \widehat {BAD} - \widehat {MAD} = {90^0} - \widehat {MAD}\).

\(\widehat {DAN} = \widehat {MAN} - \widehat {MAD} = {90^0} - \widehat {MAD}\)

\( \Rightarrow \widehat {BAM} = \widehat {DAN}\)

Xét \({\Delta }ABM\) và \({\Delta }ADN\) có:

\(AB = AD\)  (ABCD là hình vuông)

\(\widehat {BAM} = \widehat {DAN}\,\,\left( {cmt} \right)\);

\( \Rightarrow {\Delta }ABM = {\Delta }ADN\)(cạnh góc vuông – góc nhọn).

b) \({\Delta }ABM = {\Delta }ADN\,\,\left( {cmt} \right) \Rightarrow AM = AN\) (hai cạnh tương ứng) \( \Rightarrow \Delta AMN\) cân tại A.

\( \Rightarrow \) Trung tuyến AO đồng thời là đường cao \( \Rightarrow AO \bot MN \Rightarrow \widehat {AOM} = {90^0}\).

Xét tứ giác ABMO có: \(\widehat {AOM} + \widehat {ABM} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác ABMO là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).

Xét tứ giác ANDO có: \(\widehat {AON} = \widehat {ADN} = {90^0} \Rightarrow \) Hai điểm O; D cùng nhìn AN dưới góc 900\( \Rightarrow A;D\) thuộc đường tròn đường kính AN \( \Rightarrow \) Tứ giác ANDO nội tiếp đường tròn đường kính AN.

c) Vì tứ giác ABMO nội tiếp (cmt) \( \Rightarrow \widehat {BOM} = \widehat {BAM}\) (hai góc nội tiếp cùng chắn cung BM).

Tứ giác ANDO nội tiếp (cmt) \( \Rightarrow \widehat {DON} = \widehat {DAN}\) (hai góc nội tiếp cùng chắn cung BN).

\({\Delta }ABM = {\Delta }ADN\,\,\left( {cmt} \right) \)

\(\Rightarrow \widehat {BAM} = \widehat {DAN}\) (hai góc tương ứng)

\( \Rightarrow \widehat {BOM} = \widehat {DON}\). Mà 2 góc này ở vị trí hai góc đồng vị \( \Rightarrow B;D;O\) thẳng hàng.

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store