-
CHƯƠNG I : CĂN BẬC HAI - CĂN BẬC BA
-
CHƯƠNG II : HÀM SỐ BẬC NHẤT
-
CHƯƠNG III: HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG IV: HÀM SỐ BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI
-
CHƯƠNG I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- 1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
- 2. Hệ thức giữa ba cạnh của tam giác vuông
- 3. Hệ thức giữa đường cao ứng với cạnh huyền và hình chiếu của hai cạnh góc vuông trên cạnh huyền
- 4. Hệ thức diện tích
- 5. Hệ thức giữa đường cao và hai cạnh góc vuông
- Bài tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Luyện tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
-
Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- 1. Khái niệm tỉ số lượng giác của một góc nhọn
- 2. Liên hệ giữa các tỉ số lượng giác của một góc
- 3. Tỉ số lượng giác của hai góc phụ nhau
- 4. Tỉ số lượng giác của các góc đặc biệt
- 5. Tìm tỉ số lượng giác bằng máy tính cầm tay
- Bài tập - Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- Luyện tập – Chủ đề 2 : Tỉ số lượng giác của góc nhọn
-
Chủ đề 3: Hệ thức về cạnh và góc trong tam giác vuông
-
Chủ đề 4 : Ứng dụng của tỉ số lượng giác
-
Ôn tập chương 1 - Hình học 9
-
-
CHƯƠNG II : ĐƯỜNG TRÒN
-
CHƯƠNG III: GÓC VỚI ĐƯỜNG TRÒN
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
Bài tập - Chủ đề 3: Tứ giác nội tiếp
Bài 13 trang 103 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho tứ giác ABCD ngoại tiếp một đường tròn. Chứng minh hai đường tròn nội tiếp hai tam giác ABC và ACD tiếp xúc nhau.
Đề bài
Cho tứ giác ABCD ngoại tiếp một đường tròn. Chứng minh hai đường tròn nội tiếp hai tam giác ABC và ACD tiếp xúc nhau.
Phương pháp giải - Xem chi tiết
Gọi M, N lần lượt là tiếp điểm của hai đường tròn nội tiếp hai tam giác ABC và ACD với AC.
Áp dụng tính chất 2 tiếp tuyến cắt nhau chứng minh
\(\begin{array}{l}2CM = CM + CJ = AC + BC - AB\\2CN = CN + CP = AC + CD - AD\end{array}\)
Xét hiệu \(2\left( {CM - CN} \right)\), chứng minh \(2\left( {CM - CN} \right) = 0 \Rightarrow M \equiv N\).
Lời giải chi tiết
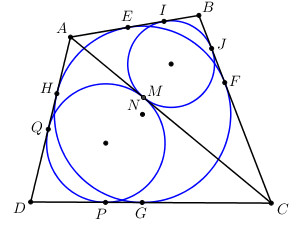
Gọi E, F, G, H lần lượt là tiếp điểm của đường tròn nội tiếp tứ giác ABCD với các cạnh AB, BC, CD, DA.
Gọi I, J, M lần lượt là tiếp điểm của đường tròn nội tiếp tam giác ABC với AB, BC, AC.
Gọi N, P, Q lần lượt là tiếp điểm của đường tròn nội tiếp tam giác ACD với AC, CD, AD.
Ta có:
\(2CM = CM + CJ = AC - AM + BC - BJ \)\(\,= AC + BC - \left( {AI + BI} \right) = AC + BC - AB\)
(Áp dụng tính chất 2 tiếp tuyến cắt nhau).
Chứng minh tương tự ta có :
\(2CN = CN + CP = AC - AN + CD - DP \)\(\,= AC + CD - \left( {AQ + DQ} \right) = AC + CD - AD\)
(Áp dụng tính chất 2 tiếp tuyến cắt nhau).
\(\begin{array}{l} \Rightarrow 2\left( {CM - CN} \right) = BC + AD - \left( {AB + CD} \right)\\ = BF + CF + AH + DH - AE - BE - CG - DG\\ = \left( {BF - BE} \right) + \left( {CF - CG} \right) + \left( {AH - AE} \right) + \left( {DH - DG} \right)\\ = 0\end{array}\)
(Áp dụng tính chất 2 tiếp tuyến cắt nhau).
\( \Rightarrow CM = CN \Rightarrow M \equiv N\).
Vậy hai đường trònnội tiếp hai tam giác ABC và ACD tiếp xúc nhau.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 14 trang 103 Tài liệu dạy – học Toán 9 tập 2
- Bài 15 trang 103 Tài liệu dạy – học Toán 9 tập 2
- Bài 16 trang 103 Tài liệu dạy – học Toán 9 tập 2
- Bài 17 trang 103 Tài liệu dạy – học Toán 9 tập 2
- Bài 18 trang 103 Tài liệu dạy – học Toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
