Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 3: Tứ giác nội tiếp

Bài 23 trang 103 Tài liệu dạy – học Toán 9 tập 2


Giải bài tập Cho tam giác ABC nội tiếp (O ; R). Gọi H là giao điểm ba đường cao AD, BE, CF. Gọi S là diện tích tam giác ABC.

Đề bài

Cho tam giác ABC nội tiếp (O ; R). Gọi H là giao điểm ba đường cao AD, BE, CF. Gọi S là diện tích tam giác ABC.

a) Chứng minh AEHF và AEDB nội tiếp.

b) Kẻ đường kính AK của đường tròn O. Chứng minh hai tam giác ABD, AKC đồng dạng và AB.AC = 2R.AD.

c) Chứng minh \(S = \dfrac{{AB.AC.BC}}{{4R}}\) .

d) Gọi M là trung điểm BC. Chứng minh tứ giác EFDM nội tiếp.

Phương pháp giải - Xem chi tiết

a) Chứng minh tứ giác AEHF có tổng hai góc đối bằng 1800.

Chứng minh tứgiaác AEDB có 2 đỉnh cùng nhìn 1 cạnh dưới các góc bằng nhau.

b) Chứng minh hai tam giác ABD, AKC đồng dạng theo trường hợp g-g, suy ra các cặp cạnh tương ứng tỉ lệ.

c) \(S = \dfrac{1}{2}AD.BC\). Rút CD ở ý b) thế vào S.

d) Chứng minh tứ giác EFDM có 2 đỉnh cùng nhìn 1 cạnh dưới các góc bằng nhau.

Lời giải chi tiết

 

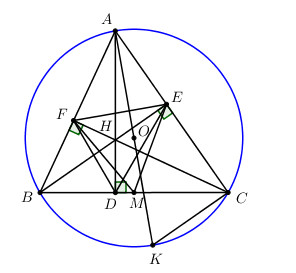
a) Xét tứ giác AEHF có: \(\widehat {AEH} + \widehat {AFH} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác AEHF là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).

Xét tứ giác AEDB có: \(\widehat {AEB} = \widehat {ADB} = {90^0}\,\,\left( {gt} \right) \Rightarrow \) 2 đỉnh E, D cùng nhìn AB dưới 1 góc 900\( \Rightarrow \) 2 điểm E; D cùng thuộc đường tròn đường kính AB. Vậy tứ giác AEDB là tứ giác nội tiếp đường tròn đường kính AB.

b) Ta có: \(\widehat {ACK} = {90^0}\) (góc nội tiếp chắn nửa đường tròn).

Xét \(\Delta ABD\) và \(\Delta AKC\) có: \(\widehat {ADB} = \widehat {ACK} = {90^0}\); \(\widehat {ABD} = \widehat {AKC}\) (2 góc nội tiếp cùng chắn cung AC).

Mà AK là đường kính của đường tròn \(\left( {O;R} \right) \Rightarrow AK = 2R \Rightarrow AB.AC = 2R.AD\).

c) Ta có \({S_{ABC}} = S = \dfrac{1}{2}AD.BC\). Mà \(AB.AC = 2R.AD \Rightarrow AD = \dfrac{{AB.AC}}{{2R}}\)

Vậy \(S = \dfrac{1}{2}.\dfrac{{AB.AC}}{{2R}}.BC = \dfrac{{AB.AC.BC}}{{4R}}\).

d) Ta có \(\widehat {BEC} = \widehat {BFC} = {90^0} \Rightarrow \) 2 điểm E, F cùng nhìn BC dưới 1 góc 900 nên 2 điểm E, F cùng thuộc đường tròn đường kính BC \( \Rightarrow \) BCEF là tứ giác nội tiếp đường tròn đường kính BC tâm M.

Xét đường tròn đường kính BC ta có: \(\widehat {EMF} = 2\widehat {ECF}\,\,\left( 1 \right)\) (góc nội tiếp bằng nửa số đo góc ở tâm cùng chắn 1 cung).

Xét tứ giác BDHF có: \(\widehat {BDH} + \widehat {BFH} = {90^0} + {90^0} = {180^0} \Rightarrow \)BDHF là tứ giác nội tiếp(Tứ giác có tổng hai góc đối bằng 1800) \( \Rightarrow \widehat {HDF} = \widehat {HBF}\) (2 góc nội tiếp cùng chắn cung HF).

Chứng minh tương tự ta có tứ giác CDHE là tứ giác nội tiếp \( \Rightarrow \widehat {HDE} = \widehat {HCE}\) (2 góc nội tiếp cùng chắn cung HE).

Ta có: \(\widehat {EDF} = \widehat {HDE} + \widehat {HDF} = \widehat {HCE} + \widehat {HDF}\).

Xét đường tròn đường kính BC có \(\widehat {HCE} = \widehat {HDF}\) (2 góc nội tiếp cùng chắn cung EF).

\( \Rightarrow \widehat {EDF} = 2\widehat {HCE} = 2\widehat {ECF}\,\,\left( 2 \right)\) .

Từ (1) và (2) \( \Rightarrow \widehat {EMF} = \widehat {ECF} \Rightarrow \) 2 đỉnh M, C cùng nhìn EF dưới góc bằng nhau. Vậy EFDM là tứ giác nội tiếp.

 Loigiaihay.com


Bình chọn:
3.8 trên 4 phiếu

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store