 Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
 Bài tập - Chủ đề 3: Tứ giác nội tiếp
Bài tập - Chủ đề 3: Tứ giác nội tiếp
Bài 3 trang 102 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Từ một điểm M nằm ngoài đường tròn (O) vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O)
Đề bài
Từ một điểm M nằm ngoài đường tròn (O) vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O) tại A. Gọi I là trung điểm của dây BC. Chứng minh AMIO là một tứ giác nội tiếp.
Phương pháp giải - Xem chi tiết
Tứ giác có tổng hai góc đối bằng 1800 là tứ giác nội tiếp.
Lời giải chi tiết
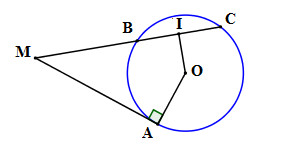
I là trung điểm của BC \( \Rightarrow OI \bot BC\) (quan hệ vuông góc giữa đường kính và dây cung)
\( \Rightarrow \widehat {OIM} = {90^0}\)
Xét tứ giác AMIO có: \(\widehat {OIM} + \widehat {OAM} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác AMIO là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
Loigiaihay.com












Danh sách bình luận