Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 3: Tứ giác nội tiếp

Bài 14 trang 103 Tài liệu dạy – học Toán 9 tập 2


Giải bài tập Một đa giác đều có n cạnh, đội dài mỗi cạnh là a. Hãy tính bán kính R và r của các đường tròn ngoại tiếp và nội tiếp đa giác đó theo a.

Đề bài

Một đa giác đều có n cạnh, đội dài mỗi cạnh là a. Hãy tính bán kính R và r của các đường tròn ngoại tiếp và nội tiếp đa giác đó theo a.

Phương pháp giải - Xem chi tiết

Tính \(\widehat {COD}\), sau đó tính sin \(\widehat {COB}\) và tan \(\widehat {COB}\), từ đó tính được R và r.

Lời giải chi tiết

 

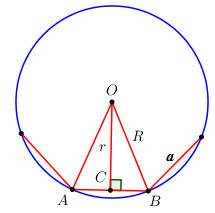
Giả sử một đa giác đều n cạnh có độ dài một cạnh là a. Gọi R là bán kính đường tròn ngoại tiếp, r bán kính đường tròn nội tiếp\( \Rightarrow OB = R;\,\,OC = r\)

\(\widehat {AOB} = \dfrac{{{{360}^0}}}{n}\)

\(\Rightarrow \widehat {COB} = \dfrac{{{{360}^0}}}{n}:2 = \dfrac{{{{180}^0}}}{n}\)

Trong \(\Delta COB\) ta có:\(\widehat {OCB} = {90^0}\)

\(\begin{array}{l}\sin \widehat {COB} = \dfrac{{CB}}{{OB}} = \dfrac{{\dfrac{a}{2}}}{R} = \dfrac{a}{{2R}} \\\Rightarrow 2R = \dfrac{a}{{\sin \widehat {COB}}} = \dfrac{a}{{\sin \dfrac{{{{180}^0}}}{n}}} \\\Rightarrow R = \dfrac{a}{{2\sin \dfrac{{{{180}^0}}}{n}}}\\\tan \widehat {COB} = \dfrac{{CB}}{{OC}} = \dfrac{{\dfrac{a}{2}}}{r} = \dfrac{a}{{2r}}\\ \Rightarrow 2r = \dfrac{a}{{\tan \widehat {COB}}} = \dfrac{a}{{\tan \dfrac{{{{180}^0}}}{n}}} \\\Rightarrow r = \dfrac{a}{{2\tan \dfrac{{{{180}^0}}}{n}}}\end{array}\)

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store