 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 2. Hệ hai phương trình bậc nhất hai ẩn
Bài 2. Hệ hai phương trình bậc nhất hai ẩn
Bài 5 trang 11 SGK Toán 9 tập 2
Đoán nhận số nghiệm của hệ phương trình sau bằng hình học:
Đề bài
Đoán nhận số nghiệm của hệ phương trình sau bằng hình học:
a) \( \left\{ \matrix{2{\rm{x}} - y = 1 \hfill \cr x - 2y = - 1 \hfill \cr} \right. \); b) \( \left\{ \matrix{2{\rm{x + }}y = 4 \hfill \cr - x + y = 1 \hfill \cr} \right. \)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Ta biến đổi các hệ phương trình đã cho về dạng \(\left\{ \begin{array}{l}y = ax + b\\y = a'x + b'\end{array} \right.\)
Gọi đường thẳng \((d):y=ax+b \) và đường thẳng \((d'): y=a'x+b' \).
+) Vẽ đường thẳng \((d)\) và \((d')\) biểu diễn tập nghiệm của hai phương trình trên cùng một hệ tọa độ.
+) Tìm giao điểm.
+) Thử lại tọa độ giao điểm đó vào hệ hai phương trình ban đầu. Nếu thỏa mãn thì là nghiệm của hệ.
Lời giải chi tiết
a) Ta có:
\(\left\{ \matrix{
2x - y = 1 \hfill \cr
x - 2y = - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = 2x - 1 \ (d)\hfill \cr
y = \dfrac{1}{2}x + \dfrac{1}{2} \ (d') \hfill \cr} \right.\)
+) Vẽ \((d)\): \(y=2x-1\)
Cho \(x = 0 \Rightarrow y = -1\), ta được \(A(0; -1)\).
Cho \(y = 0 \Rightarrow x = \dfrac{1}{2}\), ta được \(B{\left(\dfrac{1}{2}; 0 \right)}\).
Đường thẳng (d) là đường thẳng đi qua hai điểm \(A,\ B\).
+) Vẽ \((d')\): \(y=\dfrac{1}{2}x+\dfrac{1}{2}\)
Cho \(x = 0 \Rightarrow y = \dfrac{1}{2}\), ta được \(C {\left(0; \dfrac{1}{2} \right)}\).
Cho \(y = 0 \Rightarrow x = -1\), ta được \(D = (-1; 0)\).
Đường thẳng (d') là đường thẳng đi qua hai điểm \(C,\ D\).
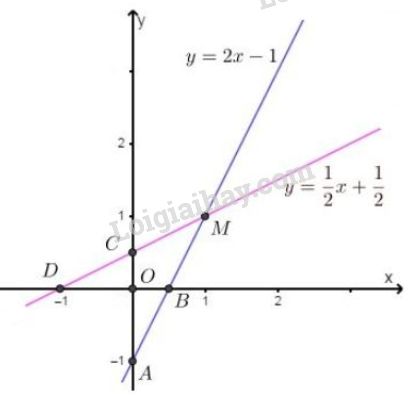
+) Quan sát hình vẽ, ta thấy hai đường thẳng cắt nhau tại điểm có tọa độ \(M( 1, 1)\).
Thay \(x = 1, y = 1\) vào các phương trình của hệ ta được:
\(\left\{ \begin{array}{l}2x - y = 1\\x - 2y = - 1\end{array} \right.\)
\(\Rightarrow\left\{ \begin{array}{l}2.1 - 1 = 1\\1 - 2.1 = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 = 1\\ - 1 = - 1\end{array} \right.\) (luôn đúng)
Vậy hệ phương trình có một nghiệm \((x; y) = (1; 1)\).
b) Ta có:
\(\left\{ \matrix{
2x + y = 4 \hfill \cr
- x + y = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = - 2x + 4 \ (d) \hfill \cr
y = x + 1 \ (d') \hfill \cr} \right.\)
+) Vẽ \((d)\): \(y=-2x+4\)
Cho \(x = 0 \Rightarrow y = 4\), ta được \(A(0; 4)\).
Cho \(y = 0 \Rightarrow x = 2\), ta được \(B(2; 0)\).
Đường thẳng (d) là đường thẳng đi qua hai điểm \(A,\ B\).
Vẽ \((d')\): \(y=x+1\)
Cho \(x = 0 \Rightarrow y = 1\), ta được \(C(0; 1)\).
Cho \(y = 0 \Rightarrow x = -1\), ta được \(D(-1; 0)\).
Đường thẳng (d') là đường thẳng đi qua hai điểm \(C,\ D\).

Quan sát hình vẽ, ta thấy hai đường thẳng cắt nhau tại điểm có tọa độ \(N(1;2)\).
Thay \(x = 1, y = 2\) vào các phương trình của hệ ta được:
\(\left\{ \begin{array}{l}2x + y = 4\\ - x + y = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2.1 + 2 = 4\\ - 1 + 2 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4 = 4\\1 = 1\end{array} \right.\) (luôn đúng)
Vậy hệ phương trình có một nghiệm \((x; y) = (1; 2)\).
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận