 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Bài 8. Diện tích xung quanh của hình chóp
Bài 8. Diện tích xung quanh của hình chóp
Bài 43 trang 122 SGK Toán 8 tập 2
Tính diện tích xung quanh,
Đề bài
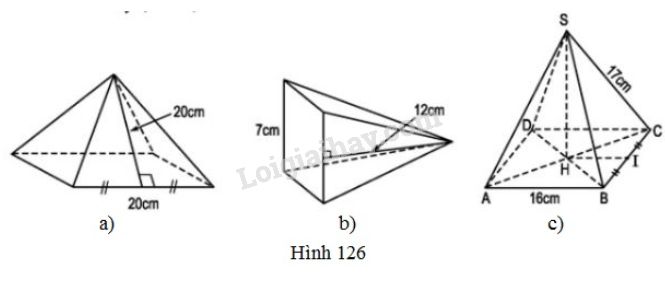
Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây.(h.126)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Tính diện tích xung quanh: \(S_{xq}= p.h \), trong đó \(p\) là nửa chu vi đáy, \(d\) là trung đoạn của hình chóp đều.
- Tính diện tích đáy theo công thức diện tích hình vuông: \(S_{hv}\) = cạnh \(\times \) cạnh.
- Tính diện tích toàn phần: \(S_{tp}= S_{xq} + S_{đ}\)
Lời giải chi tiết
+) Hình a :
Chu vi đáy là \(20.4 (cm)\)
Diện tích xung quanh của hình chóp đều là:
\(S_{xq}= p.d = \dfrac{1}{2}.20.4.20 = 800(cm^2) \)
Diện tích đáy là:
\( S_{đ} = 20^2 = 400(cm^2) \)
Diện tích toàn phần của hình chóp đều là:
\( S_{tq}= S_{xq} + S_{đ} = 800 + 400 = 1200\) \((cm^2) \)
+) Hình b:
Chu vi đáy là \(4.7 = 28 (cm)\)
Diện tích xung quanh của hình chóp đều là:
\(S_{xq}= p.d = \dfrac{1}{2}.28.12 = 168 (cm^2) \)
Diện tích đáy là:
\( S_{đ} = 7^2 = 49(cm^2) \)
Diện tích toàn phần của hình chóp đều là:
\( S_{tp}= S_{xq} + S_{đ} = 168 + 49 = 217\)\(\,(cm^2) \)
+) Hình c:
Do I là trung điểm của BC nên \(IC=\dfrac{BC}{2}=8cm\)
Tam giác SBC có SI là đường trung tuyến nên đồng thời là đường cao, xét tam giác SIC vuông tại I, theo định lý Pytago, ta có:
\(SI = \sqrt{SC^{2}- IC^{2}}\)\(=\sqrt{17^{2}- 8^{2}}= \sqrt{225} = 15(cm) \)
Hay trung đoạn \(d=SI=15cm\)
Chu vi đáy: \(16.4=64cm\)
Diện tích xung quanh của hình chóp đều là:
\(S_{xq}= p.d = \dfrac{1}{2}.64.15 = 480(cm^2) \)
Diện tích đáy là:
\( S_{đ} = 16^2 = 256(cm^2) \)
Diện tích toàn phần của hình chóp đều là:
\( S_{tp}= S_{xq} + S_{đ} = 480 + 256 = 736\) \((cm^2) \)
Loigiaihay.com












Danh sách bình luận