 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Bài 8. Diện tích xung quanh của hình chóp
Bài 8. Diện tích xung quanh của hình chóp
Bài 41 trang 121 SGK Toán 8 tập 2
Vẽ cắt và gấp miếng bìa như đã chỉ ra ở hình 55
Video hướng dẫn giải
Vẽ cắt và gấp miếng bìa như đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.
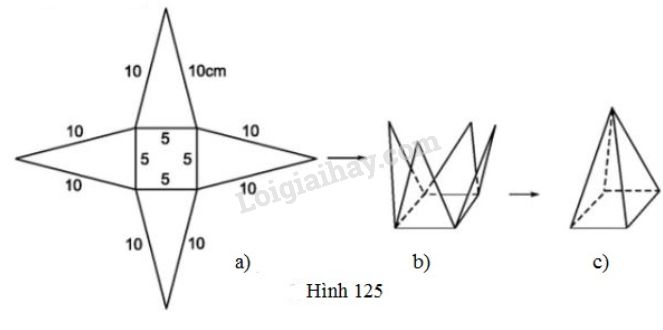
LG a.
Trong hình 125a, có bao nhiêu tam giác cân bằng nhau?
Phương pháp giải:
Áp dụng: Định nghĩa chóp tứ giác đều
Lời giải chi tiết:
Trong hình 125a có 4 tam giác cân bằng nhau.
LG b.
Sử dụng định lí Pitago để tính chiều cao ứng với đáy của mỗi tam giác.
Phương pháp giải:
Áp dụng: Định lý Py-ta-go
Lời giải chi tiết:
Đặt tên cho 1 mặt bên như hình vẽ:
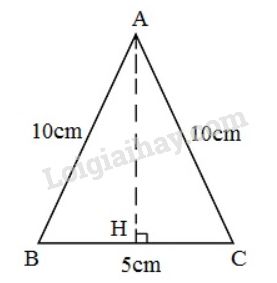
Gọi H là chân đường cao hạ từ A xuống BC, mà tam giác ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến.
Do đó \(HC=BC:2=\dfrac{5}{2}cm\)
Xét tam giác AHC vuông tại H, theo định lý Py-ta-go ta có:
\(AH = \sqrt{AC^{2}- HC^{2}}\)
\(= \sqrt{10^{2}- {\left( {\dfrac{5}{2}} \right)^2}} = \sqrt{100-\dfrac{25}{4}} \)
\(\approx 9,68\) \(cm\)
LG c.
Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu ?
Phương pháp giải:
Áp dụng:
- Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn.
- Công thức tính diện tích toàn phần: \( S_ {tp} = S_{xq}+ S_{đ}\)
Lời giải chi tiết:
Chu vi đáy của hình chóp là \(4.5 = 20 (cm).\)
Diện tích xung quanh hình chóp:
\(S_{xq} = p. d =\dfrac{1}{2}.20.9,68 = 96,8\) \( (cm^2) \)
Diện tích đáy:
\( S_{đ} = 5^2 = 25 (cm^2) \)
Diện tích toàn phần của hình chóp:
\( S_ {tp} = S_{xq}+ S_{đ} = 96,8 + 25 = 121,8\) \((cm^2) \)
Loigiaihay.com












Danh sách bình luận