Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 27 trang 88 SGK Toán 9 tập 1


Giải tam giác ABC vuông tại A, biết rằng:

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Video hướng dẫn giải

Lựa chọn câu để xem lời giải nhanh hơn

Giải tam giác \(ABC\) vuông tại \(A\), biết rằng:

LG a

\(b=10cm;\ \widehat{C}=30^{\circ}\)

Phương pháp giải:

Giải tam giác vuông là đi tìm tất cả các yếu tố (góc và cạnh) chưa biết của tam giác đó.

+) Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác \(ABC\) vuông tại \(A\) thì:

\(b=a.\sin B = a . \cos C;\)                  \(b = c. \tan B = c. \cot C;\)

\(c=a.\sin C = a. \cos B;\)                    \(c=b.\tan C = b.\cot B\).  

Lời giải chi tiết:

 Quy ước: Tam giác ABC vuông tại A có a = BC ; b = AC; c = AB

(H.a)

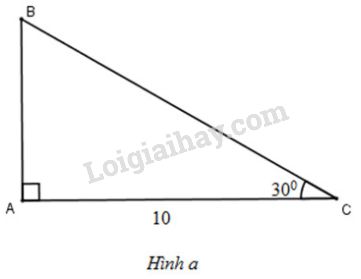
+) Ta có: \(\widehat{B} + \widehat{C}=90^{\circ} \Rightarrow \widehat{B}=90^o -30^{\circ}=60^{\circ}\)

+) Lại có 

\(AB = AC. \tan C=10.tan 30^o=\dfrac{10\sqrt 3}{3} \approx 5,77(cm)\)

\(AC=BC. \cos C \Rightarrow 10=BC. \cos 30^o \Rightarrow BC=\dfrac{10}{\cos 30^o}=\dfrac{20\sqrt 3}{3} \approx 11,55(cm)\).

LG b

\(c=10cm;\ \widehat{C}=45^{\circ}\)

Phương pháp giải:

Giải tam giác vuông là đi tìm tất cả các yếu tố (góc và cạnh) chưa biết của tam giác đó.

+) Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác \(ABC\) vuông tại \(A\) thì:

\(b=a.\sin B = a . \cos C;\)                  \(b = c. \tan B = c. \cot C;\)

\(c=a.\sin C = a. \cos B;\)                    \(c=b.\tan C = b.\cot B\).  

Lời giải chi tiết:

(H.b)

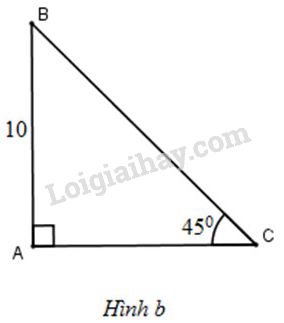
+) Xét tam giác \(ABC\) vuông tại \(A\) có \(AB=10,\ \widehat{C}=45^o\) nên \(ABC\) là tam giác vuông cân tại A \(\Rightarrow \widehat{B}=45^{\circ}; AB=AC=10(cm)\)

+) Lại có: \(AB=BC. \sin C \Rightarrow 10=BC. sin 45^o\)

\(\Rightarrow BC=\dfrac{10}{\sin 45^o}=10\sqrt 2 \approx 14,14(cm).\)

LG c

\(a=20cm;\ \widehat{B}=35^{\circ}\)

Phương pháp giải:

Giải tam giác vuông là đi tìm tất cả các yếu tố (góc và cạnh) chưa biết của tam giác đó.

+) Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác \(ABC\) vuông tại \(A\) thì:

 \(b=a.\sin B = a . \cos C;\)                  \(b = c. \tan B = c. \cot C;\)

\(c=a.\sin C = a. \cos B;\)                    \(c=b.\tan C = b.\cot B\).  

Lời giải chi tiết:

 (H.c) 

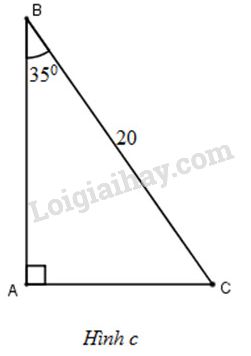
+) Ta có: \(\widehat{C}+ \widehat{B}=90^{\circ} \Rightarrow \widehat{C}= 90^o - \widehat{B}=90^o - 35^{\circ}=55^{\circ}.\) 

+) Lại có: \(AB=BC\cdot cosB=20\cdot cos35^{\circ}\approx 16,383 (cm)\)

                \(AC= BC \cdot sinB=20\cdot sin35^{\circ}\approx 11,472 (cm)\).

LG d

\(c=21cm;\ b=18cm\)

Phương pháp giải:

Giải tam giác vuông là đi tìm tất cả các yếu tố (góc và cạnh) chưa biết của tam giác đó.

+) Sử dụng định lý Pytago: Tam giác \(ABC\) vuông tại \(A\) thì \(BC^2 = AC^2 + AB^2.\)

+) Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác \(ABC\) vuông tại \(A\) thì:

 \(b=a.\sin B = a . \cos C;\)                  \(b = c. \tan B = c. \cot C;\)

\(c=a.\sin C = a. \cos B;\)                    \(c=b.\tan C = b.\cot B\).  

Lời giải chi tiết:

(H.d)

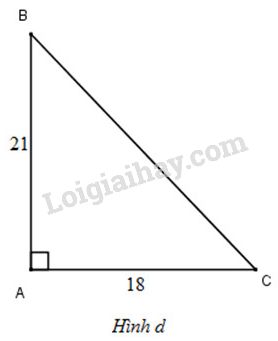
Áp dụng định lí Pytago vào tam giác vuông ABC, ta được: \(BC^2=AC^2+AB^2=18^2 +21^2=765\)

\(\Rightarrow BC = \sqrt{765}=3\sqrt{85} \approx 27,66(cm)\)

Lại có:

\(\tan B=\dfrac{AC}{AB}=\dfrac{18}{21} \approx 0,8571\)

Bấm máy tính: SHIFT tan 0,8571 \(\Rightarrow \widehat{B}\approx 41^{\circ}\)

Vì \(\widehat{C }+\widehat{B}=90^o \Rightarrow \widehat{C}= 90^o - 41^o =49^{\circ}\) 


Bình chọn:
4.5 trên 277 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store