Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 3. Liên hệ giữa phép nhân và phép khai phương

Bài 24 trang 15 SGK Toán 9 tập 1


Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ 3) của các căn thức sau:

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ \(3\)) của các căn thức sau:

\(a)\) \( \sqrt{4(1 + 6x + 9x^{2})^{2}}\) tại \(x =  - \sqrt 2 \); 

\(b)\) \( \sqrt{9a^{2}(b^{2} + 4 - 4b)}\) tại \(a =  - 2;\,\,b =  - \sqrt 3 \).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng các công thức sau: 

+) \((a+b)^2=a^2+2ab+b^2\).

+) \((a-b)^2=a^2-2ab+b^2\).

+) \( \sqrt{a.b}=\sqrt{a}.\sqrt{b}\),   với \(a ,\ b \ge 0\).

+) \(\sqrt{a^2}=\left|a\right|\).

+) Nếu \(a \ge 0\)   thì \(\left|a\right|=a\).

    Nếu \(a<0\)   thì \(\left| a\right|=-a\).

+) \(a^m. b^m=(ab)^m\),    với \(m ,\ n \in \mathbb{Z}\).

Lời giải chi tiết

a) Ta có: 

\( \sqrt{4(1 + 6x + 9x^{2})^{2}}\) \(=\sqrt {4}. \sqrt {{{(1 + 6x + 9{x^2})}^2}} \)

                                   \(=\sqrt{4}.\sqrt{(1+2.3x+3^2.x^2)^2}\)

                                   \(=\sqrt{2^2}.\sqrt{\left[1^2+2.3x+(3x)^2\right]^2}\)

                                   \(=2.\sqrt {{{\left[ {{{\left( {1 + 3x} \right)}^2}} \right]}^2}} \)

                                   \(=2.\left|(1+3x)^2\right|\)

                                   \(=2(1+3x)^2\).

 (Vì  \( (1+3x)^2 > 0 \) với mọi \(x\)  nên \(\left|(1+3x)^2\right|=(1+3x)^2  \))

Thay \(x =  - \sqrt 2 \) vào biểu thức rút gọn trên, ta được: 

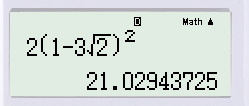
                                \( 2{\left[ {1 + 3.(-\sqrt 2) } \right]^2}=2(1-3\sqrt{2})^2\).

Bấm máy tính, ta được: \( 2{\left( {1 - 3\sqrt 2 } \right)^2} \approx 21,029\).

b) Ta có:

\( \sqrt{9a^{2}(b^{2} + 4 - 4b)} =\sqrt{3^2.a^2.(b^2-4b+4)}\)

                                  \(=\sqrt{(3a)^2.(b^2-2.b.2+2^2)}\)

                                  \(=\sqrt{(3a)^2}. \sqrt{(b-2)^2}\)

                                  \(=\left|3a\right|. \left|b-2\right| \)

Thay \(a = -2\) và \(b =  - \sqrt 3 \) vào biểu thức rút gọn trên, ta được:

\(\left| 3.(-2)\right|. \left| -\sqrt{3}-2\right| =\left|-6\right|.\left|-(\sqrt{3}+2) \right|\)

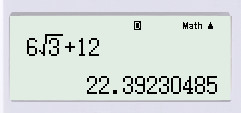
                                     \(=6.(\sqrt{3}+2)=6\sqrt{3}+12\).

Bấm máy tính, ta được: \(6\sqrt{3}+12 \approx 22,392\). 


Bình chọn:
4.5 trên 166 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store