 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
Trả lời câu hỏi 1 Bài 3 trang 105 SGK Toán 9 Tập 1
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
Đề bài
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
a) Nếu AB = CD thì OH = OK.
b) Nếu OH = OK thì AB = CD.
Video hướng dẫn giải
Lời giải chi tiết
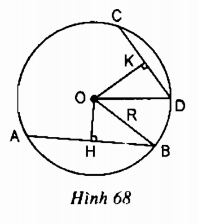
Xét đường tròn \((O)\) có
OH là một phần đường kính vuông góc với dây AB
\( \Rightarrow \) H là trung điểm của \(AB\) (Định lí) \( \Rightarrow AB{\rm{ }} = {\rm{ }}2HB\)
OK là một phần đường kính vuông góc với dây CD
\( \Rightarrow \) K là trung điểm của \(CD\) (Định lí) \( \Rightarrow CD{\rm{ }} = {\rm{ }}2KD\)
Theo mục 1: \(O{H^2} + H{B^2} = O{K^2} + K{D^2}\)
a) Nếu \(AB{\rm{ }} = {\rm{ }}CD \Rightarrow HB{\rm{ }} = {\rm{ }}KD\)
mà \(O{H^2} + H{B^2} = O{K^2} + K{D^2}\) \( \Rightarrow O{H^2} = O{K^2} \Rightarrow OH = OK\)
b) Nếu \(OH = OK \Rightarrow O{H^2} = O{K^2}\)
mà \(O{H^2} + H{B^2} = O{K^2} + K{D^2}\) \( \Rightarrow HB{\rm{ }} = {\rm{ }}KD \Rightarrow AB{\rm{ }} = {\rm{ }}CD\)
Các bài khác cùng chuyên mục












Danh sách bình luận