Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây

Bài 15 trang 106 SGK Toán 9 tập 1


Tổng hợp đề thi vào 10 tất cả các tỉnh thành trên toàn quốc

Toán - Văn - Anh

Đề bài

Cho hình \(70\) trong đó hai đường tròn cùng có tâm là \(O\). Cho biết \(AB>CD\).

Hãy so sánh các độ dài:

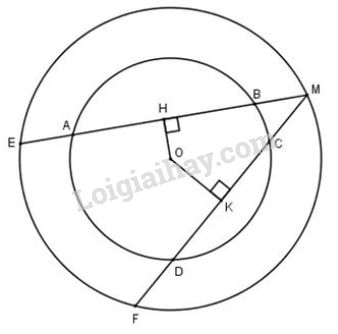
a) \(OH\) và \(OK\);

b) \(ME\) và \(MF\);

c) \(MH\) và \(MK\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+) Để so sánh hai dây, ta đi so sánh khoảng cách từ tâm đến hai dây ấy và ngược lại.

+) Sử dụng tính chất: Trong một đường tròn:

a) Dây nào lớn hơn thì dây đó gần tâm hơn.

b) Dây nào gần tâm hơn thì dây đó lớn hơn.

c) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Lời giải chi tiết

a) Xét trong đường tròn nhỏ:

Theo định lí \(2\): trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.

Theo giả thiết \(AB > CD\) suy ra \(AB\) gần tâm hơn, tức là  \(OH < OK \).

b) Xét trong đường tròn lớn:

Theo định lí \(2\): trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.

Theo câu \(a\), ta có: \(OH < OK \Rightarrow ME > MF\).

c) Xét trong đường tròn lớn:

Vì \(OH \bot ME \Rightarrow EH=MH=\dfrac{ME}{2}\) (Định lý 2 - trang 103).

Vì \(OK \bot MF \Rightarrow KF=MK=\dfrac{MF}{2}\) (Định lý 2 - trang 103). 

Theo câu \(b\), ta có: \(ME > MF \Rightarrow \dfrac{ME}{2} > \dfrac{MF}{2} \Leftrightarrow MH > MK\)

Loigiaihay.com


Bình chọn:
4.5 trên 103 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com. , cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua