 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 2 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 2 - Hình học 9
Đề bài
Gọi I là trung điểm của dây cung AB không qua tâm của đường tròn (O; R). Qua I vẽ dây cung CD.
a. Chứng tỏ \(CD ≥ AB\). Tìm độ dài nhỏ nhất, lớn nhất của các dây quanh I.
b. Cho \(R = 5cm, OI = 4cm.\) Tính độ dài dây cung ngắn nhất qua I.
c. Chứng tỏ rằng : \(\widehat {OAI} > \widehat {ODI}\)
Phương pháp giải - Xem chi tiết
- Trong hai dây của một đường tròn:
a) Dây nào lớn hơn thì dây đó gần tâm hơn.
b) Dây nào gần tâm hơn thì dây đó lớn hơn.
- Định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương các cạnh góc vuông.
- Sử dụng tỉ số lượng giác của góc nhọn.
Lời giải chi tiết
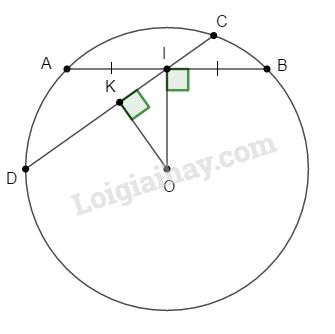
a. Kẻ \(OK ⊥ CD\), ta có: \(∆OKI\) vuông nên \(OI ≥ OK\) (cạnh huyền > cạnh góc vuông)
\(⇒ CD ≥ AB\) (định lí 2)
Dấu “=” xảy ra khi \(CD = AB.\) Do đó độ dài nhỏ nhất của CD bằng AB hay CD trùng với AB. Hiển nhiên đường kính qua I là dây lớn nhất.
b. Ta có: \(∆OIA\) vuông tại I
\( \Rightarrow AI = \sqrt {O{A^2} - O{I^2}} \)\(\;= \sqrt {{5^2} - {4^2}} = 3\,\left( {cm} \right)\)
Do đó dây cung \(AB = 6cm\)
c. \(\sin \widehat {OAI} = {{OI} \over {OA}} = {{OI} \over R};\)\(\,\sin \widehat {ODI} = {{OK} \over {OD}} = {{OK} \over R}\)
Mà \(OI > OK \Rightarrow {{OI} \over R} > {{OK} \over R}\) hay \(\sin \widehat {OAI} > \sin \widehat {ODI} \Rightarrow \widehat {OAI} > \widehat {ODI}\)
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận