Đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 Trường THCS Trung Sơn Trầm

Bài 1. (2 đ) Phân tích đa thức thành nhân tử:

a) \(x\left( {x - y} \right) + 7x - 7y\)

b) \({x^3} - 2{x^2} - 9x + 18\)

c) \(3{x^2} - 6xy + 3{y^2} - 12{z^2}\)

Bài 2. (2 điểm) 

1. Tìm \(x\) biết

a) \({x^2} - 2x = 0\)

b) \({x^2} - 7x + 12 = 0\)

2. Tìm số \(a\) để đa thức \(2{x^3} - 7{x^2} + 7x + a\) chia hết cho đa thức \(2x - 5\).

Bài 3. (2 điểm) Cho \(P = \left( {\dfrac{{x + 5}}{{x - 2}} + \dfrac{{3x}}{{x + 2}} - \dfrac{{4{x^2}}}{{{x^2} - 4}}} \right).\dfrac{{{x^2} + 2x}}{{x + 10}}\)

a) Tìm điều kiện của \(x\) để giá trị của \(P\) xác định.

b) Rút gọn \(P\).

c) Tính giá trị của \(P\), biết \({x^2} - x - 6 = 0\)

Bài 4. (3,5 điểm) Cho \(\Delta ABC\) vuông tại A \(AC = 4cm\), điểm M là trung điểm của của BC. Gọi E là điểm đối xứng với M qua AB, I là giao điểm của ME và AB. Gọi F là điểm đối xứng với M qua AC, K là giao điểm của MF và AC.

a) Chứng minh AM=IK

b) Tứ giác AMCF là hình gì? Vì sao?

c) Chứng minh A là trung điểm của EF.

d)  Tam giác vuông ABC cần có điều kiện gì để tứ giác BCKI là hình thang cân? Khi đó tính diện tích của tứ giác BCKI.

Bài 5. (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức:

\(S = {x^2} - 2xy + 6{y^2} - 12x + 2y + 45\)

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

Bài 1 (VD):

Phương pháp:

Nhóm các hạng tử kết hợp dùng hằng đẳng thức và đặt nhân tử chung.

Cách giải:

a) \(x\left( {x - y} \right) + 7x - 7y\)

\(\begin{array}{l} = x\left( {x - y} \right) + 7\left( {x - y} \right)\\ = \left( {x + 7} \right)\left( {x - y} \right)\end{array}\)

b) \({x^3} - 2{x^2} - 9x + 18\)

\(\begin{array}{l} = \left( {{x^3} - 2{x^2}} \right) - \left( {9x - 18} \right)\\ = {x^2}\left( {x - 2} \right) - 9\left( {x - 2} \right)\\ = \left( {{x^2} - 9} \right)\left( {x - 2} \right)\\ = \left( {x - 3} \right)\left( {x + 3} \right)\left( {x - 2} \right)\end{array}\)

c) \(3{x^2} - 6xy + 3{y^2} - 12{z^2}\)

\(\begin{array}{l} = \left( {3{x^2} - 6xy + 3{y^2}} \right) - 12{z^2}\\ = 3\left( {{x^2} - 2xy + {y^2}} \right) - 12{z^2}\\ = 3{\left( {x - y} \right)^2} - 12{z^2}\\ = 3\left[ {{{\left( {x - y} \right)}^2} - 4{z^2}} \right]\\ = 3\left( {x - y - 2z} \right)\left( {x - y + 2z} \right)\end{array}\)

Bài 2 (VD):

Phương pháp:

1. Phân tích VT thành tích, sử dụng \(AB = 0\) thì \(A = 0\) hoặc \(B = 0\).

2. Thực hiện chia đa thức cho đa thức, phép chia là phép chia hết nếu số dư bằng \(0\).

Cách giải:

1. Tìm \(x\) biết

a) \({x^2} - 2x = 0\)

\(x\left( {x - 2} \right) = 0\)

\(x = 0\) hoặc \(x - 2 = 0\)

\(x = 0\) hoặc \(x = 2\).

Vậy \(x = 0\) hoặc \(x = 2\).

b) \({x^2} - 7x + 12 = 0\)

\(\begin{array}{l}{x^2} - 3x - 4x + 12 = 0\\\left( {{x^2} - 3x} \right) - \left( {4x - 12} \right) = 0\\x\left( {x - 3} \right) - 4\left( {x - 3} \right) = 0\\\left( {x - 3} \right)\left( {x - 4} \right) = 0\end{array}\)

TH1: \(x - 3 = 0\)

\(\begin{array}{l}x = 0 + 3\\x = 3\end{array}\)

TH2: \(x - 4 = 0\)

\(\begin{array}{l}x = 0 + 4\\x = 4\end{array}\)

Vậy \(x = 3\) hoặc \(x = 4\).

2. Tìm số \(a\) để đa thức \(2{x^3} - 7{x^2} + 7x + a\) chia hết cho đa thức \(2x - 5\).

Ta chia \(2{x^3} - 7{x^2} + 7x + a\) cho \(2x - 5\) được:

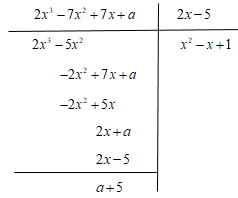
Để đa thức \(2{x^3} - 7{x^2} + 7x + a\) chia hết cho \(2x - 5\) thì \(a + 5 = 0 \Leftrightarrow a =  - 5\).

Vậy \(a =  - 5\).

Bài 3 (VD):

Phương pháp:

a) Biểu thức \(\dfrac{1}{{P\left( x \right)}}\) xác định nếu \(P\left( x \right) \ne 0\).

b) Quy đồng mẫu thức, rút gọn \(P\).

c) Tìm \(x\) thỏa mãn điều kiện rồi thay vào biểu thức rút gọn của \(P\) và tính giá trị.

Cách giải:

a) Tìm điều kiện của \(x\) để giá trị của \(P\) xác định.

ĐK: \(\left\{ \begin{array}{l}x - 2 \ne 0\\x + 2 \ne 0\\{x^2} - 4 \ne 0\\x + 10 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne  \pm 2\\x \ne 10\end{array} \right.\)

b) Rút gọn \(P\).

\(P = \left( {\dfrac{{x + 5}}{{x - 2}} + \dfrac{{3x}}{{x + 2}} - \dfrac{{4{x^2}}}{{{x^2} - 4}}} \right).\dfrac{{{x^2} + 2x}}{{x + 10}}\)

\(P = \left( {\dfrac{{x + 5}}{{x - 2}} + \dfrac{{3x}}{{x + 2}} - \dfrac{{4{x^2}}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}} \right).\dfrac{{x\left( {x + 2} \right)}}{{x + 10}}\)

\(P = \left( {\dfrac{{\left( {x + 5} \right)\left( {x + 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} + \dfrac{{3x\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} - \dfrac{{4{x^2}}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}} \right).\dfrac{{x\left( {x + 2} \right)}}{{x + 10}}\)

\(P = \left( {\dfrac{{{x^2} + 7x + 10 + 3{x^2} - 6x - 4{x^2}}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}} \right).\dfrac{{x\left( {x + 2} \right)}}{{x + 10}}\)

\(P = \dfrac{{x + 10}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}.\dfrac{{x\left( {x + 2} \right)}}{{x + 10}}\)

\(P = \dfrac{x}{{x - 2}}\)

c) Tính giá trị của \(P\), biết \({x^2} - x - 6 = 0\)

Ta có: \({x^2} - x - 6 = 0\)

\(\begin{array}{l}{x^2} - 3x + 2x - 6 = 0\\x\left( {x - 3} \right) + 2\left( {x - 3} \right) = 0\\\left( {x + 2} \right)\left( {x - 3} \right) = 0\end{array}\)

\(x + 2 = 0\) hoặc \(x - 3 = 0\)

\(x =  - 2\left( {loai} \right)\) hoặc \(x = 3\left( {TM} \right)\)

Với \(x = 3\) thì \(P = \dfrac{3}{{3 - 2}} = \dfrac{3}{1} = 3\).

Vậy với \(x = 3\) thì \(P = 3\).

Bài 4 (VD):

Phương pháp:

a) Chứng minh \(AIMK\) là hình chữ nhật suy ra hai đường chéo bằng nhau.

b) Chứng minh \(AMCF\) là hình thoi theo dấu hiệu nhận biết hai đường chéo vuông góc với nhau tại trung điểm mỗi đường.

c) Chứng minh \(A,E,F\) thẳng hàng và \(AE = AF\).

d) Sử dụng dấu hiệu: Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

Cách giải:

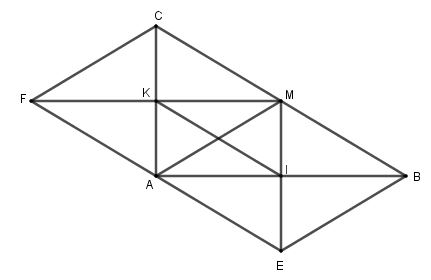
a) Chứng minh AM=IK

Điểm E đối xứng với M qua AB nên \(ME \bot AB\) tại I và \(IM = ME\).

Điểm F đối xứng với M qua AC nên \(MF \bot AC\) tại K và \(KM = KF\).

\( \Rightarrow \widehat {MKA} = \widehat {MIA} = {90^0}\).

Tứ giác \(AIMK\) có \(\widehat {MKA} = \widehat {MIA} = \widehat {KAI} = {90^0}\) nên là hình chữ nhật (dhnb)

\( \Rightarrow IK = AM\left( {t/c} \right)\) (đpcm)

b) Tứ giác AMCF là hình gì? Vì sao?

Ta có:

\(\left\{ \begin{array}{l}BA \bot AC\left( {gt} \right)\\MK \bot AC\left( {cmt} \right)\end{array} \right. \Rightarrow BA//MK\) (từ vuông góc đến song song)

Mà \(M\) là trung điểm \(BC\) nên \(K\) là trung điểm \(AC\).

Lại có \(K\) là trung điểm \(AC\) nên tứ giác \(AMCF\) có hai đường chéo \(AC,MF\) vuông góc với nhau tại trung điểm \(K\) của mỗi đường

\( \Rightarrow AMCF\) là hình thoi (dhnb).

c) Chứng minh A là trung điểm của EF.

Từ câu b, \(AMCF\) là hình thoi \( \Rightarrow AF//CM,AF = CM\) (1)

Chứng minh tương tự câu b ta được \(AMBE\) là hình thoi

\( \Rightarrow AE//BM,AE = BM\)  (2)

Từ (1) và (2) suy ra \(A,E,F\) thẳng hàng và \(AE = AF\).

Vậy \(A\) là trung điểm \(EF\).

d) Tam giác vuông ABC cần có điều kiện gì để tứ giác BCKI là hình thang cân? Khi đó tính diện tích của tứ giác BCKI.

Ta có:

\(I,K\) lần lượt là trung điểm của \(AB,AC\) nên \(IK\) là đường trung bình của tam giác \(ABC\)

\( \Rightarrow IK//BC \Rightarrow IKCB\) là hình thang.

Để \(IKCB\) là hình thang cân thì \(\widehat {KCB} = \widehat {IBC}\) hay \(\widehat {ACB} = \widehat {ABC}\)

Do đó tam giác \(ABC\) vuông cân tại \(A\).

\( \Rightarrow AB = AC = 4cm\) \( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AB.AC\) \( = \dfrac{1}{2}.4.4 = 8\left( {c{m^2}} \right)\)

Lại có \(AI = \dfrac{1}{2}AB = \dfrac{1}{2}.4 = 2\left( {cm} \right),\) \(AK = \dfrac{1}{2}AC = \dfrac{1}{2}.4 = 2\left( {cm} \right)\)

\( \Rightarrow {S_{\Delta AIK}} = \dfrac{1}{2}AI.AK\) \( = \dfrac{1}{2}.2.2 = 2\left( {c{m^2}} \right)\)

\( \Rightarrow {S_{IKCB}} = {S_{\Delta ABC}} - {S_{\Delta AIK}}\) \( = 8 - 2 = 6\left( {c{m^2}} \right)\)

Vậy \({S_{IKCB}} = 6\left( {c{m^2}} \right)\).

Bài 5 (VD):

Phương pháp:

Sử dụng các hằng đẳng thức \({\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2ab + 2ac + 2bc\) và \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\)

Đưa về dạng: \({A^2} + {B^2} + m \ge m\)

Dấu “=” xảy ra khi: \(A = B = 0\)

Cách giải:

Ta có: \(S = {x^2} - 2xy + 6{y^2} - 12x + 2y + 45\)

\( = \left( {{x^2} + {y^2} + 36 - 2xy - 12x + 12y} \right)\) \( + 5{y^2} - 10y + 9\)

\( = {\left( {x - y - 6} \right)^2} + 5{\left( {y - 1} \right)^2} + 4\)

Vì \({\left( {x - y - 6} \right)^2} \ge 0;{\left( {y - 1} \right)^2} \ge 0\) với mọi \(x;y\)

Nên \(S = {\left( {x - y - 6} \right)^2} + 5{\left( {y - 1} \right)^2} + 4 \ge 4\) với mọi \(x;y\)

Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}x - y - 6 = 0\\y - 1 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 7\end{array} \right.\)

Vậy giá trị nhỏ nhất của \(S\) là \(4 \Leftrightarrow x = 7;y = 1\).

Hết

Loigiaihay.com