Đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GDĐT Bình Chánh

Câu 1. (2,5 điểm) Thực hiện các phép tính:

a) $\left( {2x + 3} \right)\left( {x - 2} \right) - {\left( {3x - 1} \right)^2}$

b) $\left( {4x - 3} \right)\left( {4x + 3} \right) + {\left( {2 - 3x} \right)^2}$

c) $\dfrac{{x + 3}}{x} - \dfrac{x}{{x - 3}} + \dfrac{9}{{{x^2} - 3x}}$

Câu 2. (1,5 điểm) Phân tích các đa thức sau thành nhân tử: 

a) ${x^2} - 9{y^2} - x + 3y$

b) $4{x^2} - 4x + 1 - {y^2}$

Câu 3. (1,5 điểm)

a) Tìm $x$ biết ${\left( {x + 7} \right)^2} - 3x - 21 = 0$

b) Tìm giá trị lớn nhất của biểu thức $A = 6 + 8x - 8{x^2}$

Câu 4. (1 điểm) Nhà trường tổ chức giải bóng đá mini mừng Xuân cho học sinh khối lớp 8, mỗi lớp cử một đội tham dự, mỗi đội lần lượt thi đấu với đội của lớp bạn một lần.

a) Viết biểu thức đại số tính tổng số trận thi đấu của khối lớp 8 nếu có $x\left( {x \in {\mathbb{Z}^ + }} \right)$ đội tham dự.

b) Nếu tổng số trận đấu là 10 thì khối lớp 8 có bao nhiêu đội tham dự?

Câu 5. (3,5 điểm) Cho $\Delta ABC$ vuông tại A $\left( {AB < AC} \right)$. Gọi M là trung điểm BC.

a) Biết $AB = 6cm,AM = 5cm$. Tính BC, AC.

b) Gọi D, E lần lượt là hình chiếu của M lên AB, AC. Chứng minh ADME là hình chữ nhật.

c) Gọi F đối xứng với M qua E, chứng minh AMCF là hình thoi.

d) Kẻ đường cao AH của tam giác ABC, chứng minh $\Delta DHE$ vuông tại H.

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

Câu 1 (VD):

Phương pháp:

a, b) Sử dụng hằng đẳng thức khai triển và rút gọn biểu thức.

c) Quy đồng, rút gọn các phân thức.

Cách giải:

a) $\left( {2x + 3} \right)\left( {x - 2} \right) - {\left( {3x - 1} \right)^2}$

$\begin{array}{l} = \left( {2{x^2} + 3x - 4x - 6} \right) - \left( {9{x^2} - 6x + 1} \right)\\ = 2{x^2} - x - 6 - 9{x^2} + 6x - 1\\ =  - 7{x^2} + 5x - 7\end{array}$

b) $\left( {4x - 3} \right)\left( {4x + 3} \right) + {\left( {2 - 3x} \right)^2}$

$\begin{array}{l} = {\left( {4x} \right)^2} - {3^2} + \left( {4 - 2.2.3x + 9{x^2}} \right)\\ = 16{x^2} - 9 + 4 - 12x + 9{x^2}\\ = 25{x^2} - 12x - 5\end{array}$

c) $\dfrac{{x + 3}}{x} - \dfrac{x}{{x - 3}} + \dfrac{9}{{{x^2} - 3x}}$ (ĐK: $x \ne 0,x \ne 3$)

$\begin{array}{l} = \dfrac{{x + 3}}{x} - \dfrac{x}{{x - 3}} + \dfrac{9}{{x\left( {x - 3} \right)}}\\ = \dfrac{{\left( {x + 3} \right)\left( {x - 3} \right)}}{{x\left( {x - 3} \right)}} - \dfrac{{{x^2}}}{{x\left( {x - 3} \right)}} + \dfrac{9}{{x\left( {x - 3} \right)}}\\ = \dfrac{{{x^2} - 9 - {x^2} + 9}}{{x\left( {x - 3} \right)}}\\ = \dfrac{0}{{x\left( {x - 3} \right)}}\\ = 0\end{array}$

Câu 2 (VD):

Phương pháp:

Nhóm các hạng tử kết hợp dùng hằng đẳng thức và đặt nhân tử chung.

Cách giải:

a) ${x^2} - 9{y^2} - x + 3y$

$\begin{array}{l} = \left[ {{x^2} - {{\left( {3y} \right)}^2}} \right] - \left( {x - 3y} \right)\\ = \left( {x - 3y} \right)\left( {x + 3y} \right) - \left( {x - 3y} \right)\\ = \left( {x - 3y} \right)\left( {x + 3y - 1} \right)\end{array}$

b) $4{x^2} - 4x + 1 - {y^2}$

$\begin{array}{l} = \left( {4{x^2} - 4x + 1} \right) - {y^2}\\ = {\left( {2x - 1} \right)^2} - {y^2}\\ = \left( {2x - 1 - y} \right)\left( {2x - 1 + y} \right)\\ = \left( {2x - y - 1} \right)\left( {2x + y - 1} \right)\end{array}$

Câu 3 (VD):

Phương pháp:

a) Phân tích vế trái thành nhân tử, sử dụng $AB = 0$ thì $A = 0$ hoặc $B = 0$.

b) Biến đổi $A$ về dạng $A = a{\left( {bx \pm c} \right)^2} + d$ với $a < 0$, từ đó đánh giá GTLN của $A$.

Cách giải:

a) Tìm $x$ biết ${\left( {x + 7} \right)^2} - 3x - 21 = 0$

$\begin{array}{l}{\left( {x + 7} \right)^2} - \left( {3x + 21} \right) = 0\\{\left( {x + 7} \right)^2} - 3\left( {x + 7} \right) = 0\\\left( {x + 7} \right)\left( {x + 7 - 3} \right) = 0\\\left( {x + 7} \right)\left( {x + 4} \right) = 0\end{array}$

$x + 7 = 0$ hoặc $x + 4 = 0$

$x =  - 7$ hoặc $x =  - 4$.

Vậy $x =  - 7$ hoặc $x =  - 4$.

b) Tìm giá trị lớn nhất của biểu thức $A = 6 + 8x - 8{x^2}$

Ta có:

$\begin{array}{l}A =  - 8{x^2} + 8x + 6\\A =  - 2\left( {4{x^2} - 4x - 3} \right)\\A =  - 2\left[ {{{\left( {2x} \right)}^2} - 2.2x.1 + {1^2} - 4} \right]\\A =  - 2\left[ {{{\left( {2x - 1} \right)}^2} - 4} \right]\\A =  - 2{\left( {2x - 1} \right)^2} + 8\end{array}$

Vì ${\left( {2x - 1} \right)^2} \ge 0$ với mọi $x$ nên $- 2{\left( {2x - 1} \right)^2} \le 0$

$\Rightarrow  - 2{\left( {2x - 1} \right)^2} + 8 \le 0 + 8 = 8$ hay $A \le 8$.

Vậy GTLN của $A$ bằng $8$ khi:

$\begin{array}{l}{\left( {2x - 1} \right)^2} = 0\\2x - 1 = 0\\2x = 1\\x = \dfrac{1}{2}\end{array}$

Câu 4 (VD):

Phương pháp:

a) Tính số trận đấu tạo thành khi mỗi đội thi đấu với các đội còn lại.

Lập luận suy ra số trận đấu có được.

b) Cho số trận đấu bằng $10$ và tìm $x$.

Cách giải:

a) Viết biểu thức đại số tính tổng số trận thi đấu của khối lớp 8 nếu có $x\left( {x \in {\mathbb{Z}^ + }} \right)$ đội tham dự.

Đội 1 thi đấu với $x - 1$ đội còn lại ta được $x - 1$ trận.

Đội 2 thi đấu với $x - 1$ đội còn lại ta được $x - 1$ trận.

…

Đội $x$ thi đấu với $x - 1$ đội còn lại ta được $x - 1$ trận.

Do đó có $x\left( {x - 1} \right)$ trận đấu.

Tuy nhiên mỗi trận đấu ở trên đều được tính $2$ lần nên ssoo trận đấu thực tết là: $\dfrac{{x\left( {x - 1} \right)}}{2}$.

Vậy có $\dfrac{{x\left( {x - 1} \right)}}{2}$ trận đấu.

b) Nếu tổng số trận đấu là 10 thì khối lớp 8 có bao nhiêu đội tham dự?

Vì có $10$ trận đấu nên ta có: $\dfrac{{x\left( {x - 1} \right)}}{2} = 10$

$\begin{array}{l}x\left( {x - 1} \right) = 10.2\\{x^2} - x = 20\\{x^2} - x - 20 = 0\\{x^2} - 5x + 4x - 20 = 0\\x\left( {x - 5} \right) + 4\left( {x - 5} \right) = 0\\\left( {x - 5} \right)\left( {x + 4} \right) = 0\\x - 5 = 0\\x = 5\left( {TM} \right)\end{array}$

(vì $x + 4 > 0$)

Vậy khối 8 có tất cả là $5$ đội tham dự.

Bài 5 (VD):

Phương pháp:

a) Sử dụng tính chất: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền và định lý Pytago

b) c) Sử dụng dấu hiệu nhận biết hình bình hành, hình thoi, hình chữ nhật

d) Sử dụng tính chất: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền và tính chất tam giác cân

Cách giải:

Cho $\Delta ABC$ vuông tại A $\left( {AB < AC} \right)$. Gọi M là trung điểm BC.

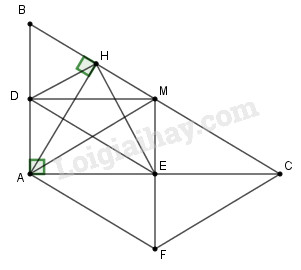
a) Biết $AB = 6cm,AM = 5cm$. Tính BC, AC.

Vì tam giác ABC vuông tại A có AM là đường trung tuyến nên $AM = \dfrac{1}{2}BC$ $\Rightarrow BC = 2AM = 2.5 = 10cm$

Xét tam giác vuông ABC, theo định lý Pytago ta có:

$\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Rightarrow A{C^2} = B{C^2} - A{B^2}\\ \Rightarrow A{C^2} = {10^2} - {6^2}\\ \Rightarrow A{C^2} = 64\\ \Rightarrow AC = 8cm\end{array}$

b) Gọi D, E lần lượt là hình chiếu của M lên AB, AC. Chứng minh ADME là hình chữ nhật.

Vì D, E lần lượt là hình chiếu của M lên AB, AC nên $MD \bot AB,ME \bot AC$ hay $\widehat {ADM} = \widehat {MEA} = {90^0}$

Xét tứ giác $ADME$ có $\widehat {DAE} = \widehat {ADM} = \widehat {MEA} = {90^0}$ nên ADME là hình chữ nhật (dhnb)

c) Gọi F đối xứng với M qua E, chứng minh AMCF là hình thoi.

Vì tam giác ABC vuông có AM là đường trung tuyến ứng với cạnh huyền nên $AM = MC = MB = \dfrac{{BC}}{2}$

Suy ra tam giác MAC cân tại M có ME là đường cao nên ME cũng là đường trung tuyến

Suy ra E là trung điểm của AC

Xét tứ giác AMCF có E vừa là trung điểm EC, vừa là trung điểm MF (do F đối xứng với M qua E)

Nên AMCF có hai đường chéo giao nhau tại trung điểm mỗi đường nên AMCF hình bình hành (dhnb)

Lại có $ME \bot AC\left( {cmt} \right)$ nên $MF \bot AC$, do đó hình bình hành AMCF có hai đường chéo vuông góc nên nó là hình thoi (dhnb)

d) Kẻ đường cao AH của tam giác ABC, chứng minh $\Delta DHE$ vuông tại H.

Xét tam giác ABH vuông tại H có HD là đường trung tuyến ứng với cạnh huyền nên $HD = BD = \dfrac{{AB}}{2}$  suy ra tam giác HBD cân tại D, do đó: $\widehat B = \widehat {BHD}$  (1)

Xét tam giác ACH vuông tại H có HE là đường trung tuyến ứng với cạnh huyền nên $HE = EC = \dfrac{{AC}}{2}$  suy ra tam giác HEC cân tại E, do đó: $\widehat {ACB} = \widehat {EHC}$ (2)

Xét tam giác ABC vuông tại A nên $\widehat B + \widehat {ACB} = {90^0}$ (3)

Từ (1), (2), (3) ta có: $\widehat {BHD} + \widehat {EHC} = \widehat B + \widehat {ACB}$ $= {90^0}$

Suy ra $\widehat {DHE} = {180^0} - \left( {\widehat {DHB} + \widehat {EHC}} \right)$ $= {90^0}$

Nên tam giác $DHE$ vuông tại $H.$

Hết